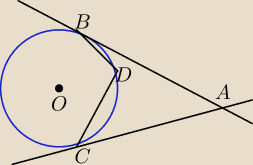
 Proste AB i AC są styczne w punktach B i C do okręgu o środku w punkcie O.
Punkt D leży na łuku BC, wewnątrz trójkąta ABC jak na rysunku powyżej.
Wykaż, że suma |∡ABD| + |∡ACD| jest stała (tzn. nie zależy od położenia punktu D na łuku BC).
Czy teza zadania będzie prawdziwa, jeśli punkt D będzie leżał na łuku BC, na zewnątrz trójkąta
ABC?
Proste AB i AC są styczne w punktach B i C do okręgu o środku w punkcie O.
Punkt D leży na łuku BC, wewnątrz trójkąta ABC jak na rysunku powyżej.
Wykaż, że suma |∡ABD| + |∡ACD| jest stała (tzn. nie zależy od położenia punktu D na łuku BC).
Czy teza zadania będzie prawdziwa, jeśli punkt D będzie leżał na łuku BC, na zewnątrz trójkąta
ABC?
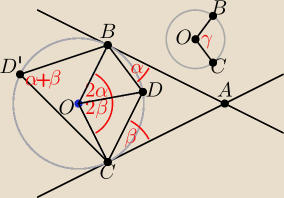 Trzeba tu skorzystać z twierdzeń o kącie dopisanym i o kącie wpisanym (tu kątami dopisanymi
są kąty ABD i ACD, kątem wpisanym jest kąt BD'C, a także zauważyć, że:
Trzeba tu skorzystać z twierdzeń o kącie dopisanym i o kącie wpisanym (tu kątami dopisanymi
są kąty ABD i ACD, kątem wpisanym jest kąt BD'C, a także zauważyć, że:
| 1 | ||
|∡BOC| = γ, |∡BOC| = 2α + 2β, |∡BD'C| = | γ = α + β | |
| 2 |