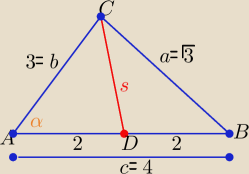
Planimetria Kamila: W trójkącie ABC dane są długości boków : IABI= 4 cm IBCI= √3 cm IACI= 3 cm a) Oblicz cos kąta BAC oraz tg kąta BAC b) Oblicz pole trójkąta ABC c) oblicz długość odcinka łączącego wierzchołek C ze środkiem boku AB Prosiłabym o rozwiązanie bo nie rozumiem jak mam to zrobić

Eta: c²>a²+b² −−− to trójkąt jest ostrokątny 16>9+3 −−− trójkąt ABC jest ostrokątny

	b2+c2−a2
a) z tw. kosinusów cosα=		= .........
	2bc

sinα= +√1−cos²α= .........

	sinα
tgα=		=......
	cosα

	1
b) P(ABC)=		*b*c*sinα=..........
	2

c) z tw. kosinusów s²= |Ad|²+b²−2b*|AD|*cosα=........ dokończ obliczenia ...

Kamila: Bardzo dziękuję za pomoc