Wyznacz te wartości Matejko: Wyznacz te wartości x dla których ciąg arytmetyczny o wyrazach y−x,^y_x, xy jest malejący zacząłem ^2y_x=y−x−xy

	x2
y=		x=/−2 i 1
	x2+x−2

x2
	<0
x2+x−2

(x²)(x²+x−2)<0 i wyszło mi że x∊(−2;0)U(0;1) ale to jest źle proszę o pomoc

wredulus_pospolitus: a skąd wyszło założenie, że 'y' < 0

wredulus_pospolitus: x= x

	x2
y =
	x2+x−2

i teraz:

	−x+2		x		y		x3
y−x =		>		=		>		= x*y
	x2+x−2		x2+x−2		x		x2+x−2

wredulus_pospolitus: bo właśnie te nierówności sa warunkiem na to, że ten ciąg będzie malejący

Matejko: nie rozumiem po i teraz:..

Matejko: tej ostatniej linijki

Matejko:

Eta: No to tak x≠0 i z def. ciągu arytm.

y		y		x2		x2
	−y+x=xy−		⇒ y=		=
x		x		x2+x−2		(x−1)(x+2)

	y		x2−1		(x−1)(x+1)
i r <0 ⇒ xy−		<0 ⇒ y(		)<0⇒		<0
	x		x		x

	x2		(x−1)(x+2)
to:		*		<0 dla x ≠0 i x≠1
	(x−1)(x+2)		x

	x(x+1)
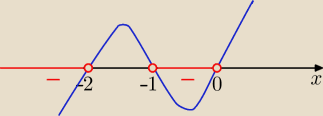
		<0 ⇒ x(x+1)(x+2)<0 ⇒ x∊(−∞,−2) U (−1,0)
	x+2

pozdrawiam

Eta:

	(x−1)(x+1)
Poprawiam chochlika w drugiej linijce ( ⇒ y*		<0
	x

Matejko: jak ci wyszła ta ostatnia linijka? nie czaje mi się poskracało i wychodzi sam x<0

Eta: W przedostatniej linijce znów chochlik

	x2		(x−1)(x+1)
to:		*		<0
	(x−1)(x+2)		x