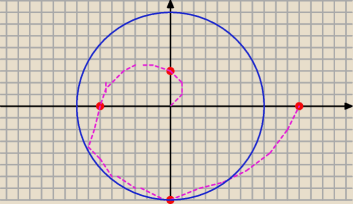
Liczby zespolone Maslanek: Liczby zespolone Wyznaczyć zbiór {z∊C/{0}: Arg(z)≤|z|} Czy można postąpić w ten sposób? Wiemy, że 0≤Arg(z)≤2π Niech z=x+iy; x,y∊R Wtedy |z|=√x²+y² Rozpatrzmy nierówność: Arg(z)≤|z| Jeżeli 2π≤|z|, to na pewno nierówność jest spełniona, skąd x²+y²=(2π)² Teraz rozpatrując kolejno coraz dalsze wartości dla kolejnych liczb z Arg(z) mielibyśmy pewnego ślimaczka zaczynającego się od (0,0) (bez punktu) do kolejno (0,π/2); (−π,0); (0,−3π/2); (2π;0) Jakby to wyglądało − rysunek Nie mieści się W każdym razie koło powinno dochodzić do (2π,0). I zbiór, który by nas interesował, to ten na zewnątrz ślimaka oraz cała prawa część prostej y=0 Jak to wygląda? Wolfram podpowiada tak: http://www.wolframalpha.com/input/?i=%7Cz%7C%3E%3DArg%28z%29. Ale tutaj Arg(z) jest wzięty od −π do π z tego co mi się wydaje. Co z moim mysleniem?

Mila: To masz spiralę Archimedesa?

Maslanek: A co to?

Maslanek: Ale wygląda dość logicznie Po przejściu na współrzędne biegunowe coś takiego powinienem dostać?