.
bezendu:
Bryły.
Ma ktoś jakiś link, gdzie pokazane są wszystkie przekątne, przekroje itp w bryłach ?
Dopiero zaczynam bryły i taki link bardzo by mi pomógł. Osobiście nie znalazłem nic takiego.
21 sty 20:36
bezendu: ?
21 sty 20:51
Ajtek:
Cześć
bezendu 
. A tutaj nie wystarczająco masz? Tzn na naszej stronce?
21 sty 21:25
bezendu:
Zdecydowanie za mało.
21 sty 21:30
21 sty 21:31
Mila:
Wrzucaj problemy, pomożemy.
21 sty 21:31
Ajtek:
A z czym masz problemy?
21 sty 21:31
Ajtek:
Witaj
Mila 
21 sty 21:31
bezendu:
Ogólnie potrzebuję dobrej teorii, nie wiem jak te kąty padają w bryłach , chodzi np o kąt
dwuścienny ?
21 sty 21:33
Ajtek:
W jakiej bryle? I jaka płaszczyzna ma go wyznaczyć

.
21 sty 21:35
bezendu:
Graniastosłup prawidłowy np.
21 sty 21:36
Mila:
Cześć Ajtek. Witam miło.
21 sty 21:36
Ajtek:
A jaka płaszczyzna ma go wyznaczyć?
21 sty 21:36
bezendu:
Jutro wrócę do tematu, dziś już niestety muszę udostępnić komputer. Dobranoc.
21 sty 21:39
Ajtek:
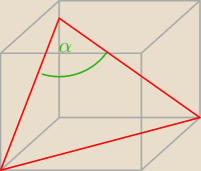
Kąt dwuścienny pomiędzy sąsiednimi ścianami bocznymi, wyznaczony przez płaszczyznę przechodzącą
przez średnicę podstawy, i dowolny punkt leżący na krawędzi bocznej

.
21 sty 21:41
Mila:
Nie, to nie jest kąt dwuścienny.
22 sty 14:53
Mila:
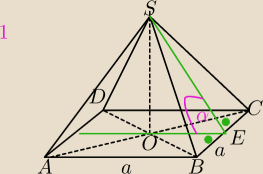
OE⊥BC i SE⊥BC
α− kat między płaszczyzną podstawy i scianą boczną ostrosłupa prawidłowego czworokatenego
22 sty 14:58
Ajtek:
Masz rację
Mila 
.
22 sty 15:01
Mila:
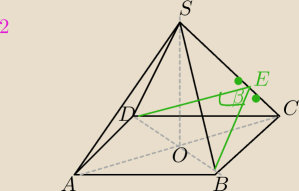 DE⊥ SC i BE ⊥ SC
DE⊥ SC i BE ⊥ SC
β−kąt między sąsiednimi ścianami bocznymi ostrosłupa prawidłowego czworokątnego
22 sty 15:03
Mila:
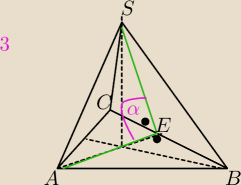 AE ⊥BC i SE ⊥ BC
AE ⊥BC i SE ⊥ BC
α− kat między płaszczyzną podstawy i ścianą boczną ostrosłupa prawidłowego trójkątnego.
22 sty 15:07
Mila:
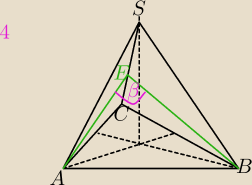 AE ⊥SC i BE ⊥ SC
AE ⊥SC i BE ⊥ SC
β−kąt między sąsiednimi ścianami bocznymi ostrosłupa prawidłowego trójkątnego
22 sty 15:12
bezendu: Dziękuję teraz już mi się rozjaśniło.
22 sty 15:49
bezendu:
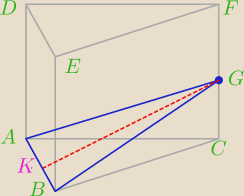
Dany jest graniastosłup prawidłowy trójkątny ABCDEF o podstawach ABC i DEF i krawędziach
bocznych AD ,BE i CF. Punkt G jest środkiem krawędzi CF . Długość krawędzi podstawy AB jest
równa 12, a pole trójkąta ABG jest równe 12
√31.Oblicz objętość tego graniastosłupa
ΔABG jest równoramienny ?
|AB|=12 P
ΔABG=12
√31
|KG|−wysokość trójkąta ABG
12*0,5*|KG|=12
√31
6|KG|=12
√31
|KG|=2
√31
|BG|=4
√10
|CG|=4
V=288
√3
?
22 sty 18:25
bezendu: ?
22 sty 20:03
Mila:
Dobrze.
22 sty 20:42
bezendu:
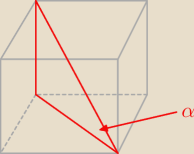
Oblicz sinus kąta między przekątną sześcianu a jego płaszczyzną podstawy.
sinα=U{
√3{3} chodzi o ten kąt ?
Wiem, że banalne ale wolę się upewnić ?
22 sty 20:53
Eta:


22 sty 20:53
Ajtek:
O ten kąt chodzi

.
22 sty 20:54
bezendu:
Witaj
Eta 
22 sty 20:54
Ajtek:
Eta mnie ubiegła

. Witaj
Eta 
.
22 sty 20:54
Mila:
Witajcie!

22 sty 21:15
bezendu:
Witaj
Mila 
22 sty 21:20
bezendu:
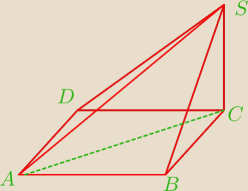
Podstawą ostrosłupa ABCDS jest prostokąt ABCD o bokach długości |AB | = 7 i |BC | = 14 .
Krawędź CS jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt 50∘
. Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość.
|AC|=7
√5
CS=7
√5*tg50
0
Mam tak zostawić ?
22 sty 22:09
Mila:
Jeśli daja taki kąt, to chcą sprawdzic, czy potrafisz odczytać wartość funkcji w tablicach.
| | 686√5 | | 686√5 | |
= |
| tg50o≈ |
| *......... |
| | 3 | | 3 | |
22 sty 22:15
bezendu:
A czy błędem będzie jak zamiast CS=7√5tg50 napisze, że ≈19 ?
22 sty 22:17
Mila:
Raczej zrób to na końcu, aby podać wartość dokładną V (z tg50) i przybliżoną.
22 sty 22:46
bezendu:
Dziękuję.
22 sty 22:50
bezendu:
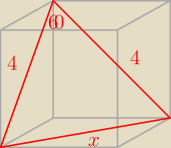
W prostopadłościanie poprowadzono z jednego wierzchołka przekątne ścian bocznych, obie o
długości 4. Wiedząc, że kąt między tymi przekątnymi ma miarę 60
∘ , oblicz pole powierzchni
tego prostopadłościanu
x
2=4
2+4
2−(2*4*4*co60
0)
x
2=16
x=4
a=2
√2
P
c=48 j
2 ?
23 sty 19:50
Eta:
bez tw. kosinusów

Ten trójkąt jest
równoboczny o boku dł.
4
( bo jest równoramienny o kącie między ramionami 60
o
23 sty 19:58
bezendu:
Ale mój sposób też ok ?
23 sty 20:00
Eta:
też

23 sty 20:00
bezendu:

dziękuję.
23 sty 20:03
23 sty 20:04
bezendu:
Oj chyba nie zasłużyłem

23 sty 20:05
Eta:
Na jedno z nich... "uważaj"

23 sty 20:06
bezendu: 1 po lewej ?
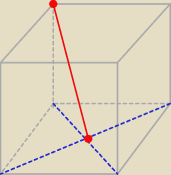
Odległość wierzchołka sześcianu od przekątnej sześcianu (do której dany wierzchołek nie należy)
jest równa 4 cm.
Może ktoś narysować ?
23 sty 20:08
Eta:
23 sty 20:14
bezendu:
Dziękuję.
23 sty 20:15
Eta:

23 sty 20:16
Eta:
Wiesz,że mi troszkę "podpadłeś" ?

23 sty 20:17
bezendu:
Kiedy ?

23 sty 20:18
bezendu:
Chodzi o ''p'' ?
23 sty 20:20
5-latek: A ktos niedawno pisal ze nie ma wyobrazni przestrzeennej

23 sty 20:22
Eta:
O "p "
23 sty 20:22
bezendu:
No to przepraszam, już więcej się to nie pojawi

23 sty 20:24
Ajtek:
Zajumał "
p"


23 sty 20:24
Eta:
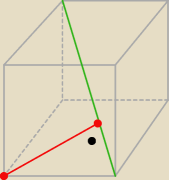
Ajjj to zły rysunek

( od przekątnej sześcianu , a nie przekątnej ściany
23 sty 20:27
bezendu: 
23 sty 20:28
Eta:
Tak, tak

ten ostatni rys.
23 sty 20:29
bezendu:
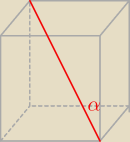
Przekątna prostopadłościanu ma długość ...i tworzy z dwoma ścianami prostopadłościanu kąty α i
β
Gdzie jest ten β ?

23 sty 20:37
52: Narysuj przekątne ścian bocznych i kąty pomiędzy przekątnymi a twoją czerwoną linią dadzą
te kąty o które chodzi
23 sty 20:39
Mila:
Źle, to jest kąt między przekątną a krawędzią.
Masz zaznaczyć kąt między przekątną a jej rzutem prostokątnym ....
Zobacz jeden przypadek u Marcina i resztę spróbuj sam.
23 sty 20:41
52:
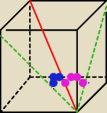
Coś takiego niebieski i różowy
23 sty 20:41
23 sty 20:42
52: Aha, przepraszam za zamieszanie ...

23 sty 20:43
Mila:
Dobrze, 52,
23 sty 20:44
bezendu:
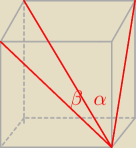
?
23 sty 20:46
Eta:
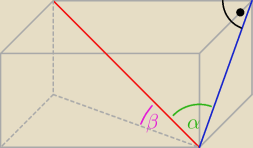
23 sty 20:47
bezendu: Dziękuję.
23 sty 20:49
Mila:
Bezendu 20:46 dobrze, Szkoda, że bez oznaczeń wierzchołków, chciałabym wiedzieć, czy
widzisz Δ prostokątne z tymi przekątnymi, bo to jest ważne .
[Z{Eta]] ładnie przewróciła bryłę, wtedy widać rzut.
23 sty 20:55
bezendu:
Właśnie z niektórymi rzutami mam jeszcze problem, bo nie wiem gdzie ten kąt prosty jest.
23 sty 21:00
Mila:
Oblicz objętość graniastosłupa prawidłowego trójkątnego,
w którym krawędź podstawy ma długość 10,
a przekątna ściany bocznej tworzy z sąsiednią ścianą kąt o mierze 30 ∘ .
23 sty 21:04
bezendu:
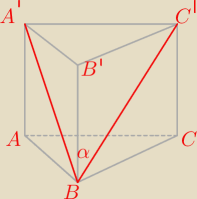
?
23 sty 21:11
Mila:
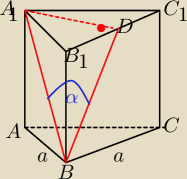
23 sty 21:17
bezendu:
A czemu BC' jest źle ?
23 sty 21:18
Eta:
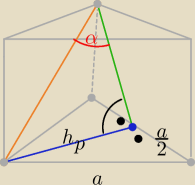
23 sty 21:22
bezendu:
Jak teraz obliczyć wysokość ?
23 sty 21:28
Eta:
Oblicz długość
zielonego odcinka
| | a | |
i z tw. Pitagorasa H2= z2−( |
| )2 |
| | 2 | |
lub długość
brązowego odcinka i H
2=
b2−a
2
23 sty 21:32
bezendu:
brązowy odcinek ma 100√3
H2=(100√3)2−102
H=10√299 ?
23 sty 21:37
bezendu: ?
23 sty 21:48
23 sty 22:03
bezendu:
Jak mam zauważyć te kąty proste ? Nie chodzi akurat o ten przykład tylko ogólnie ?
23 sty 22:05
Mila:
Modele, bryłki szkieletowe.
23 sty 22:07
5-latek: Ja wlasnie zakupilem wczoraj patyczki do liczenia i plasteline

23 sty 22:09
Mila:
Bardzo dobry pomysł.
23 sty 22:10
bezendu:
Dziękuję, a na rysunku jak to wiedzieć ?
Na ferie mam zamiar sobie wydrukować 400 zadań z brył, ale w takim tępię to raczej nie zrobię

23 sty 22:15
Mila:
Masz jakiś podręcznik? Powinny być przykładowe zadania.
Pracowicie będziesz tu wpisywał i nauczysz się tych kątów.
23 sty 22:25
bezendu: Mam, matematyka z plusem.
Od jakich brył zacząć?
23 sty 22:27
Mila:
Graniastosłupy. Oglądaj rysunki.
Twierdzenie o trzech prostopadłych.
23 sty 22:40
bezendu: Ok, dziękuję.
23 sty 22:42
5-latek: Kiedys Ci polecalem taka ksiazke Czeslaw DYtz Geometria dla samoukow
czesc druga to stereometria. sam teraz z niej korzystam . masz tam wszystko ladnie opisane
23 sty 22:46
bezendu:
Przejrzałem, analizowałem i nadal nic.

27 sty 19:08
bezendu:
Jak to twierdzenie o 3 prostopadłych wykorzystać w zadaniach. Bo jakoś mam z tym problem
27 sty 20:23
bezendu:
Jakieś zadania, żeby to zacząć zauważać ?
27 sty 21:15
Mila:
Będziesz wyciągał wniosek o prostopadłości odcinków. ( np. dla ustalenia Δ prostokątnych)
27 sty 21:16
bezendu: No tak tylko, w tych bryłach trzeba szukać kąta prostego a ja go tam nadal nie widzę. Przez co
nie mogę zrozumieć niektórych zadań z P a co dopiero z R.
27 sty 21:18
Mila:
Pisz , podpowiem. Pokażę na rysunku.
27 sty 21:20
bezendu:
Podstawą graniastosłupa prostego jest trójkąt prostokątny o przyprostokątnych mających długości
1 i √3 . Podaj miary kątów między sąsiednimi ścianami bocznymi tego graniastosłupa.
27 sty 21:24
Mila:
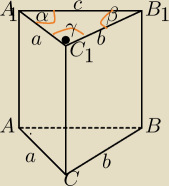
Tutaj to są kąty ΔABC, bo ściany boczne są prostopadłe do płaszczyzny podstawy.
γ=90
o
reszte liczysz.
27 sty 21:44
bezendu:
to będzie trójkąt szczególny 30,60,90 ?
27 sty 21:47
bezendu: ?
27 sty 22:15
bezendu: ?
27 sty 22:39
mea:
tak
27 sty 22:43
bezendu:
Dzięki.
27 sty 22:44
Mila:
Załóż nowy wątek, bo przy tej liczbie zapisów trudno się zorientować czy zaglądac.
27 sty 22:54
bezendu:
Czyli tutaj w tym zadaniu trzeba po prostu wyliczyć kąty w podstawie trójkąta ?
27 sty 22:57
mea:
dokładnie tak
27 sty 22:58
bezendu:
Dziękuję jeszcze raz.
27 sty 22:59
 . A tutaj nie wystarczająco masz? Tzn na naszej stronce?
. A tutaj nie wystarczająco masz? Tzn na naszej stronce?

 .
.
 Kąt dwuścienny pomiędzy sąsiednimi ścianami bocznymi, wyznaczony przez płaszczyznę przechodzącą
przez średnicę podstawy, i dowolny punkt leżący na krawędzi bocznej
Kąt dwuścienny pomiędzy sąsiednimi ścianami bocznymi, wyznaczony przez płaszczyznę przechodzącą
przez średnicę podstawy, i dowolny punkt leżący na krawędzi bocznej  .
.
 OE⊥BC i SE⊥BC
α− kat między płaszczyzną podstawy i scianą boczną ostrosłupa prawidłowego czworokatenego
OE⊥BC i SE⊥BC
α− kat między płaszczyzną podstawy i scianą boczną ostrosłupa prawidłowego czworokatenego
 .
.
 DE⊥ SC i BE ⊥ SC
β−kąt między sąsiednimi ścianami bocznymi ostrosłupa prawidłowego czworokątnego
DE⊥ SC i BE ⊥ SC
β−kąt między sąsiednimi ścianami bocznymi ostrosłupa prawidłowego czworokątnego
 AE ⊥BC i SE ⊥ BC
α− kat między płaszczyzną podstawy i ścianą boczną ostrosłupa prawidłowego trójkątnego.
AE ⊥BC i SE ⊥ BC
α− kat między płaszczyzną podstawy i ścianą boczną ostrosłupa prawidłowego trójkątnego.
 AE ⊥SC i BE ⊥ SC
β−kąt między sąsiednimi ścianami bocznymi ostrosłupa prawidłowego trójkątnego
AE ⊥SC i BE ⊥ SC
β−kąt między sąsiednimi ścianami bocznymi ostrosłupa prawidłowego trójkątnego
 Dany jest graniastosłup prawidłowy trójkątny ABCDEF o podstawach ABC i DEF i krawędziach
bocznych AD ,BE i CF. Punkt G jest środkiem krawędzi CF . Długość krawędzi podstawy AB jest
równa 12, a pole trójkąta ABG jest równe 12√31.Oblicz objętość tego graniastosłupa
ΔABG jest równoramienny ?
|AB|=12 PΔABG=12√31
|KG|−wysokość trójkąta ABG
12*0,5*|KG|=12√31
6|KG|=12√31
|KG|=2√31
Dany jest graniastosłup prawidłowy trójkątny ABCDEF o podstawach ABC i DEF i krawędziach
bocznych AD ,BE i CF. Punkt G jest środkiem krawędzi CF . Długość krawędzi podstawy AB jest
równa 12, a pole trójkąta ABG jest równe 12√31.Oblicz objętość tego graniastosłupa
ΔABG jest równoramienny ?
|AB|=12 PΔABG=12√31
|KG|−wysokość trójkąta ABG
12*0,5*|KG|=12√31
6|KG|=12√31
|KG|=2√31
 Oblicz sinus kąta między przekątną sześcianu a jego płaszczyzną podstawy.
sinα=U{√3{3} chodzi o ten kąt ?
Wiem, że banalne ale wolę się upewnić ?
Oblicz sinus kąta między przekątną sześcianu a jego płaszczyzną podstawy.
sinα=U{√3{3} chodzi o ten kąt ?
Wiem, że banalne ale wolę się upewnić ?


 .
.

 . Witaj Eta
. Witaj Eta  .
.


 Podstawą ostrosłupa ABCDS jest prostokąt ABCD o bokach długości |AB | = 7 i |BC | = 14 .
Krawędź CS jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt 50∘
. Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość.
|AC|=7√5
CS=7√5*tg500
Podstawą ostrosłupa ABCDS jest prostokąt ABCD o bokach długości |AB | = 7 i |BC | = 14 .
Krawędź CS jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt 50∘
. Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość.
|AC|=7√5
CS=7√5*tg500
 W prostopadłościanie poprowadzono z jednego wierzchołka przekątne ścian bocznych, obie o
długości 4. Wiedząc, że kąt między tymi przekątnymi ma miarę 60∘ , oblicz pole powierzchni
tego prostopadłościanu
x2=42+42−(2*4*4*co600)
x2=16
x=4
a=2√2
Pc=48 j2 ?
W prostopadłościanie poprowadzono z jednego wierzchołka przekątne ścian bocznych, obie o
długości 4. Wiedząc, że kąt między tymi przekątnymi ma miarę 60∘ , oblicz pole powierzchni
tego prostopadłościanu
x2=42+42−(2*4*4*co600)
x2=16
x=4
a=2√2
Pc=48 j2 ?
 Ten trójkąt jest równoboczny o boku dł. 4
( bo jest równoramienny o kącie między ramionami 60o
Ten trójkąt jest równoboczny o boku dł. 4
( bo jest równoramienny o kącie między ramionami 60o

 dziękuję.
dziękuję.

 ?
? 










 Ajjj to zły rysunek
Ajjj to zły rysunek  ( od przekątnej sześcianu , a nie przekątnej ściany
( od przekątnej sześcianu , a nie przekątnej ściany

 ten ostatni rys.
ten ostatni rys.
 Przekątna prostopadłościanu ma długość ...i tworzy z dwoma ścianami prostopadłościanu kąty α i
β
Gdzie jest ten β ?
Przekątna prostopadłościanu ma długość ...i tworzy z dwoma ścianami prostopadłościanu kąty α i
β
Gdzie jest ten β ? 
 Coś takiego niebieski i różowy
Coś takiego niebieski i różowy

 ?
?







 Tutaj to są kąty ΔABC, bo ściany boczne są prostopadłe do płaszczyzny podstawy.
γ=90o
reszte liczysz.
Tutaj to są kąty ΔABC, bo ściany boczne są prostopadłe do płaszczyzny podstawy.
γ=90o
reszte liczysz.