wartość Kapsel : Znajdź największą i najmniejszą wartość funkcji f(x)= √3sinx+cosx

	π
y=2sin(x+		)
	6

Wiem ze największa wartość to 2 i najmniejsza −2, ale jakich argumentów?

Mila: 1) y=√3sinx+cosx przekształcamy wzór

	√3		1
y=2*(		sinx+		*cosx)⇔
	2		2

	π		π
y=2*(sinx*cos		+sin		*cosx)⇔
	6		6

	π
y=2*sin(x+		)
	6

	π
−1≤sin(x+		)≤1 /*2
	6

	π
−2≤2sin(x+		)≤2
	6

Dla jakich argumentów?

	π
sin (x+		)=−1
	6

	π		3π
x+		=		+2kπ
	6		2

	3π		π
x=		−		+2kπ
	2		6

	4π
x=		+2kπ
	3

Rozwiąż

	π
sin (x+		)=1
	6

Kapsel :

	3π
Witam, trochę późno piszę. nie wiem za bardzo z kąd się wzięło		?
	2

dla sinx=−1

	π
x=−		+2kπ
	2

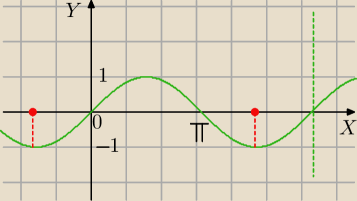Mila: To jest to samo co u Ciebie, ja podaję rozwiązanie w przedziale <0,2π> Jeżeli w Twoim podstawisz k=1, to masz :

	−π		3π
x=		+2π=
	2		2

Znasz dobrze wykres sinx?

Kapsel :

	π
aha, to mam pytanie ( tak mnie uczyli w szkole), jak sin jest ujemny np: −		to muszę ten
	2

wynik dodać do π?

Mila: Możesz zostawić jak podałeś

	−π
sinx=−1⇔x=		+2kπ,
	2

albo "przejść" do natępnego przedziału dodając 2π, bo taki jest okres sinus(x), popatrz na wykres. Nie wiem, czy o to Ci chodzi. Resztę jutro. Dobranoc.