. Piotr 10: W ostrosłupie prawidłowym czworokątnym wysokość ma długość H i tworzy z krawędzią boczną kąt 60⁰. Oblicz pole przekroju tego ostrosłupa płaszczyzną zawierającą przekątną podstawy i równoległą do jednej z krawędzi bocznych. Nie wiem jak narysować pole przekroju ostrosłupa zbytnio, mogę prosić o pomoc ?

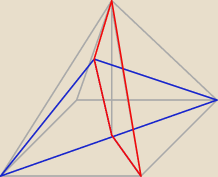
Godzio: Rysunek taki sobie, ale jakoś jest Niebieski obszar − szukany przekrój Czerwony obszar − trapez, chciałem przez to pokazać, że wysokość tego przekroju jest równoległa do odpowiedniej krawędzi bocznej (kąt między przekrojem, a płaszczyzną podstawy jest taki sam jak między krawędzią boczną i płaszczyzną podstawy)

Piotr 10: Dzięki, eh ciężko z tymi przekrojami

Piotr 10:

	H2√3
Czy pole tego przekroju to P=		?
	9

Piotr 10: ?

Godzio: Ile CI wyszła podstawa i wysokość przekroju ?

Piotr 10:

	2H√3
podstawa
	3

	H
wysokość
	3

ale pewnie źle

Godzio: Podstawa na pewno jest źle, bo to jest przekątna podstawy ostrosłupa, a on ja równa 2H√3

Piotr 10: Po raz kolejny źle tg użyłem, wszystko mi się myli, podstawa teraz dobrze mam 2√3H

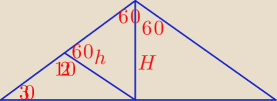
Godzio: d = 2H√3 Mamy trójkąt równoboczny, więc h = H

Piotr 10: a wysokość przekroju ?

Piotr 10: Godzio możesz zerknąć? Kompletnie sobie nie radzę z zadaniami ,które dostałem

Godzio: Ten rysunek jest odnoście wysokości h = H (trójkąt składa się z krawędzi bocznych i przekątnej podstawy)

Piotr 10: Ja to tego nie widzę . Ale dobra, jutro spróbuję, dzięki za pomoc

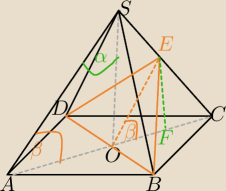
Mila: H=|SO| α=60^o β=30^o W ΔSOE:

	AO
tg60o=
	H

√3		AO
	=
1		H

|AO|=√3*H |DB|=2√3*H

	1
OE=		|AS| z tw. Talesa.
	2

|AS|=2H |OE|=H Masz odpowiedź?

Piotr 10: Mila nie mam odpowiedzi niestety. Chciałbym się zapytać czy robić takie zadania z przekrojami w ostrosłupach, bo mam trochę ich od pani ze szkoły, ale po prostu nie umiem tego robić. Problem zaczyna się z rysunkiem przekroju. I nie wiem czy robić te zadania czy nie, skoro i tak nie wiem jak to robić. Może takie coś na maturze wystąpić ?

Eta: Na rozszerzeniu? .... więcej niż pewne, że będą

Mila: Więcej niż pewne, będą.

Piotr 10: :(

Mila: Rozwiązywać z przekrojami.

Godzio: W stereometrii ważne jest, żeby sobie przenosić wszystkie interesujące Cię figury przenosić na płaszczyznę (tutaj powinieneś narysować sobie szukany przekrój i ten przekrój co ja rysowałem, składający się z dwóch krawędzi bocznych i przekątnej podstawy )