ciaglosc funkcji
ola: Zbadać ciągłość funkcji:
a) f(x)= 2x dla x∊(−∞, 1)
x2−1 dla x∊<1,2>
6x−1 dla x∊(2, +∞)
obliczam granice lim x−>1 z lewej striony i wychodzi granica −∞
granica lim x−> 1 wychodzi granica 1
lim x−>2 wychodzi 3
lim x−−>2 z prawej striny wychodzi 0 wiec z jakiej paki na fucnkja jest ciagla lewostronnie w
punnkcie 1?
21 sty 12:54
kika:
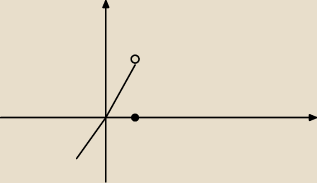
21 sty 15:20
Basia: a to jakim cudem ?
lim
x→1−f(x) = lim
x→1−2x = 2*1 = 2
lim
x→1+f(x) = lim
x→1+(x
2−1) = 1−1 = 0
w punkcie x=1 funkcja nie jest ciągła
lim
x→2−f(x) = lim
x→2−(x
2−1} = 4−1 = 3
| | 1 | |
limx→2+f(x) = limx→2+6x−1 = 6*2−1 = 6* |
| = 3 |
| | 2 | |
w punkcie x=2 funkcja jest ciągła
21 sty 15:42
kika:
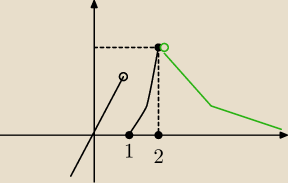
I graficznie nie ma wątpliwości , poprzedni rys dotyczył x=1
21 sty 15:48

 I graficznie nie ma wątpliwości , poprzedni rys dotyczył x=1
I graficznie nie ma wątpliwości , poprzedni rys dotyczył x=1