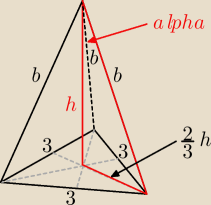
 Wysokość ostrosłupa prawidłowego trójkątnego tworzy z krawędzią boczną tego ostrosłupa kąt α
taki, że cos α = 0.8. Krawędź podstawy ma długość 3 cm. Oblicz pole powierzchni całkowitej
tego ostrosłupa.
Mam pytanie czy dobrze narysowałem i wszystko zaznaczyłem oraz jak do tego się zabrać ?
Można z jedynki trygonometrycznej obliczyć sin i wyjdzie 35 więc krawędź boczna b=5, a
podstawa czerwonego trójkąta 3 ?
Wysokość ostrosłupa prawidłowego trójkątnego tworzy z krawędzią boczną tego ostrosłupa kąt α
taki, że cos α = 0.8. Krawędź podstawy ma długość 3 cm. Oblicz pole powierzchni całkowitej
tego ostrosłupa.
Mam pytanie czy dobrze narysowałem i wszystko zaznaczyłem oraz jak do tego się zabrać ?
Można z jedynki trygonometrycznej obliczyć sin i wyjdzie 35 więc krawędź boczna b=5, a
podstawa czerwonego trójkąta 3 ?
| 3√3 | 2 | |||
2) hp= | ⇒ | h=√3 | ||
| 2 | 3 |
| 4 | ||
3) cosα= | = | |
| 5 |
| 4 | 9 | |||
sin2α=1−( | )2= | i sinα>0 | ||
| 5 | 25 |
| 3 | √3 | |||
sinα= | = | |||
| 5 | b |
| 5√3 | ||
b= | ||
| 3 |
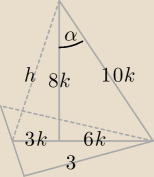
| 1 | ||
Można i tak: h = √64k2 + 9k2 = k√73 i | *3√3 = 9k ⇒ k = | |
| 2 |
| 1 | 1 | |||
Pole całkowite P = | *3*9k + 3* | *3h = ... | ||
| 2 | 2 |