udowadnianie w czworokącie Kassia: Wykaż, że pole dowolnego czworokąta ABCD jest równe 1/2 AC x BD sin α, gdzie AC i BD są przekątnymi tego czworokąta, natomiast α jest miarą kąta między tymi przekątnymi.

M:

M:

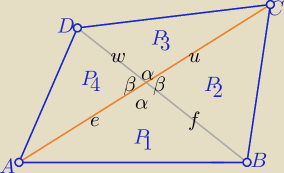
Misia: α+β=180^o , β= 180^o−α to sinβ= sinα i |AC|= e+u , |BD|= f+w

	ef		fu		uw		we
P1=		sinα, P2=		sinα , P3=		sinα, P4=		sinα
	2		2		2		2

P=P₁+P₂+P₃+P₄

	sinα		sinα
P=		(ef+fu+uw+we) =		( e+u)(f+w)
	2		2

	1
P=		|AC|*|BD|*sinα
	2