matematykaszkolna.pl
Równanie Kapsel :
 tgx 
Wyznacz wszystkie rozwiązania równania
− 2sinx=0
 cosx 
 π π 5π 
wyszło mi x=
lub x=−=
lub =
. może ktoś sprawdzić czy dobrze?
 4 4 4 
20 sty 15:23
Patronus:
sinx 1 
*
− 2sinx = 0
cosx cosx 
sinx − 2sinxcos2x 
= 0
cos2x 
sinx − 2sinx(1−sin2x) 
= 0 |cos2x
cos2x 
sinx − 2sinx + 2sin3x = 0 2sin3x − sinx =0 sinx(2sin2x − 1) = 0
 1 
sinx = 0 lub sin2x =
 2 
x = kπ, k∊Z lub
 √2 
sinx =
 2 
 π 
x =
+ 2kπ, k∊Z
 4 
to mi wyszło inaczej emotka
20 sty 15:30
J:
 1 
Równanie wyjściowe prowadzi do równania: sinx(1−2cosx)=0 , czyli sinx = 0 v cosx=
 2 
20 sty 15:31
J: Wycofuję to co napisałem ... bzdura emotka
20 sty 15:32
Kapsel : ja robiłem tak:
tgx 
− 2sinx=0
cosx 
sinx 
cosx 
 
= 2sinx
cosx 
sinx 2sinx 1 
=
I *
cos2x 1 sinx 
1 
=2
cos2x 
2cos2=1
 √2 √2 
cosx=
lub cosx=−
 2 2 
20 sty 15:40
Patronus:
 √2 
a racja, jeszcze −
mi uciekło...
 2 
20 sty 15:42
Kapsel : mój wynik jest dobry?
20 sty 15:43
J:
 1 
Nie wolno Ci pomnozyć obustronnie przez:
, przecież sinx może byc równy "0"
 sinx 
20 sty 15:43
Patronus: Kapsel, Twój wynik nie jest dobry bo zabrakło w nim rozwiązania sinx = 0
 √2 
ale mój jest niekompletny bo zabrakło w nim rozwiązania sinx = −
emotka
 2 
20 sty 15:46
Kapsel :
sinx 
=2sinx
cos2x 
sinx 
=2sinx
1−sin2x 
2sinx−2sin3x=sinx −sinx(2sinx2−1)=0
 √2 √2 
sinx=0 sinx=
sinx= −
 2 2 
 π 3π 
x=kπ, x=
+2kπ x=
+2kπ i co ujemnym sinusem?
 4 4 
20 sty 15:52
Patronus: i to jest ok emotka
20 sty 15:54
Kapsel :
 √2 
ale jak rozwiązać sinx=x=−
?
 2 
20 sty 15:56
Patronus:
 5π 7π 
no to będzie
+ 2kπ lub
+2kπ
 4 4 
20 sty 15:59
Kapsel :
 7π 9π 
zamiast
powinno być chyba
 4 4 
20 sty 16:05
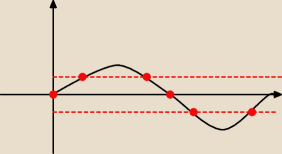Patronus: rysuneko tyle rozwiązań mamy mieć i o tu na osi umieszczone.
20 sty 16:08