Napisz równanie stycznych do okręgu o i równoległych do prostej k proszę o pomoc: Napisz równanie stycznych do okręgu o i równoległych do prostej k o:x2+y2−2x−15=0 k; y=−3x

Eta: równanie tych stycznych maja postać : y = ax +b gdzie a = −3 ( bo maja być równoległe do prostej y = −3x więc równanie stycznych jest: y = −3x +b , zatem należy wyznaczyć wartość "b" można to zrobić tak: 1/ sposób rozwiązać układ równań okręgu i prostej y = −3x +b i nałożyć warunek : Δ= 0 , i podać wówczas wartość "b" 2/ sposób (o wiele szybszy , a czas rozwiązywania zad. np.na maturze jest drogocenny wyznaczamy środek i promień tego okręgu S( 1,0) r= 4 bo: x² +y² −2x −15=0 to ( x −1)² +y² = 16 odległość srodka S od stycznych = r= 4 korzystając ze wzoru: Ax +By +C = 0 P(x_o,y_o)

	IA*xo+B*yo+CI
d=
	√A2+B2

zatem: równanie prostej: 3x +y −b =0 i S( 1,0) i d= 4

3*1+0−bI
	= 4
√9+1

to: I3 − bI= 4√10 to: 3 −b = 4√10 lub 3 −b = −4√10 b = 3 −4√10 v x = 3+4√10 więc równania stycznych są: y= −3x +3− 4√10 i y = −3x +3 +4√10 PS: policz tym pierwszym sposobem , przekonasz się,że wyniki są te same, ale więcej czasu zabierają obliczenia .

Kingaaaaaa: super, dzięki wielkie!

aaa: o: x²+y²−2x+12y+28=0; k: y=−x

Kibume:

	IA*xo+B*yo+CI|
Mam pytanie odnośnie tej części zadania, w której stosujemy wzór d=
	√A2+B2

to a i b bierzemy z postaci y=ax+b, tak? W takim razie skąd wezmę C?

Qulka: z postaci y=ax+b trzeba zrobić ax−y+b=0 wtedy A=a B=−1 C=b

Kibume: Dzięki. Czy mogła/mógł byś sprawdzić czy wykonałem dobrze podobne zadanie? "Napisz równanie stycznych do okręgu o i równoległych do prostej k o:x²+y²−14x+24=0 k: y=−0,75x" Obliczałem tym drugim sposobem. Wyznaczyłem postać: (x−7)²+y²=25, zatem punkt S=(7;0), r=5. Następnie skorzystałem ze wzoru, o który pytałem i wyszło mi: y=−0,75x−1,25 lub y=−0,75x+11,5 Czy dobrze wykonałem to zadanie?

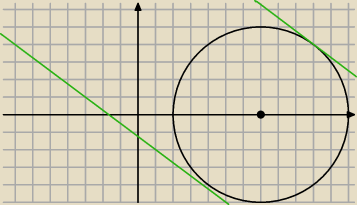
Qulka: jak widać dobrze

Kibume: Super! Dzięki wielkie za sprawdzenie