Badanie funkcji 2222: Badanie funkcji y=(1−x)*x2

Janek191: Czy y = ( 1 − x)*x² ?

2222: tak

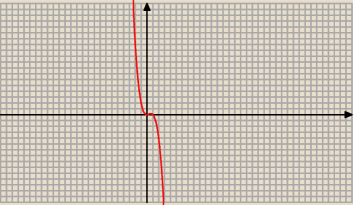
Janek191: Czyli y = x² − x³ D = R lim x → −∞ ( x² − x³ ) = +∞ lim x → + ∞ ( x² − x³ ) = lim x → ∞ x²*( 1 − x) = − ∞ y' = 2x − 3 x² y' = 0 ⇔ 2x − 3 x² = 0 ⇔ x*( 2 − 3x) = 0 ⇔ x = 0 lub x =²₃ y(0) = 0

	4		8		4
y( 23) = (23)2 − (23)3 =		−		=		> 0
	9		27		27

y" = 2 − 6 x y"( 0) = 2 > 0 i y" ( ²₃) = − 2 < 0 Funkcja ma w punkcie x = 0 minimum lokalne , a w punkcie x = ²₃ maksimum lokalne. y ' = 2x − 3 x² = x*( 2 − 3x) ⇒ dla x ∊ ( 0 ; ²₃ ) jest y ' > 0 , więc dana funkcja rośnie w tym przedziale, a w R \ ( 0; ²₃) maleje.