Twierdzenie o okręgu w trójkącie
Wilku:
Cześć!
Mam następujące twierdzenie które starałem się udowodnić:
W każdy trójkąt można wpisać okrąg.
Dowód:
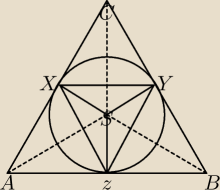
Niech punktem przecięcia dwusiecznych kątów trójkąta ΔABC będzie środek okręgu (o środku S).
Zauważmy, że okrąg w trójkącie będzie ograniczony tylko punktami styczności okręgu z bokami
trójkąta, jeżeli |XS|=|YS|=|ZS|=R to w dany trójkąt możemy wpisać okrąg. Równości tych
odcinków dowodzi równoramienność trójkątów ΔZYS i ΔXZS. Natomiast równoramienności tych
trójkąt dowodzi fakt, iż [1. no właśnie, i tutaj nie wiem, wiem, że to prawda, bo inaczej
byśmy tego okręgu nie wpisali, ale nie wiem jak dowieść, że kąty ∡YZS, ∡ZYS i im odpowiadająca
para po drugiej stronie osi symetrii są równe] [2. Jeżeli dowiedzie się tego faktu to tak
naprawdę jest to koniec dowodu gdyż jest to dowód na powyższe rozważania... czy dobrze
rozumuję?]
i trzecie pytanie... Jak ten dowód sformalizować?
Dziękuję za przeczytanie i proszę o pomoc!
 Cześć!
Mam następujące twierdzenie które starałem się udowodnić:
W każdy trójkąt można wpisać okrąg.
Dowód:
Niech punktem przecięcia dwusiecznych kątów trójkąta ΔABC będzie środek okręgu (o środku S).
Zauważmy, że okrąg w trójkącie będzie ograniczony tylko punktami styczności okręgu z bokami
trójkąta, jeżeli |XS|=|YS|=|ZS|=R to w dany trójkąt możemy wpisać okrąg. Równości tych
odcinków dowodzi równoramienność trójkątów ΔZYS i ΔXZS. Natomiast równoramienności tych
trójkąt dowodzi fakt, iż [1. no właśnie, i tutaj nie wiem, wiem, że to prawda, bo inaczej
byśmy tego okręgu nie wpisali, ale nie wiem jak dowieść, że kąty ∡YZS, ∡ZYS i im odpowiadająca
para po drugiej stronie osi symetrii są równe] [2. Jeżeli dowiedzie się tego faktu to tak
naprawdę jest to koniec dowodu gdyż jest to dowód na powyższe rozważania... czy dobrze
rozumuję?]
i trzecie pytanie... Jak ten dowód sformalizować?
Dziękuję za przeczytanie i proszę o pomoc!
Cześć!
Mam następujące twierdzenie które starałem się udowodnić:
W każdy trójkąt można wpisać okrąg.
Dowód:
Niech punktem przecięcia dwusiecznych kątów trójkąta ΔABC będzie środek okręgu (o środku S).
Zauważmy, że okrąg w trójkącie będzie ograniczony tylko punktami styczności okręgu z bokami
trójkąta, jeżeli |XS|=|YS|=|ZS|=R to w dany trójkąt możemy wpisać okrąg. Równości tych
odcinków dowodzi równoramienność trójkątów ΔZYS i ΔXZS. Natomiast równoramienności tych
trójkąt dowodzi fakt, iż [1. no właśnie, i tutaj nie wiem, wiem, że to prawda, bo inaczej
byśmy tego okręgu nie wpisali, ale nie wiem jak dowieść, że kąty ∡YZS, ∡ZYS i im odpowiadająca
para po drugiej stronie osi symetrii są równe] [2. Jeżeli dowiedzie się tego faktu to tak
naprawdę jest to koniec dowodu gdyż jest to dowód na powyższe rozważania... czy dobrze
rozumuję?]
i trzecie pytanie... Jak ten dowód sformalizować?
Dziękuję za przeczytanie i proszę o pomoc!