całka oznaczona właściwa.
Klaudia18:
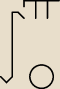
całka oznaczona właściwa.
∫ (0 do π)
∫x
2 sinx dx =
mam mały problem z wynikiem powinno być π
2 − 4
19 sty 17:09
MQ: 2 razy przez części
19 sty 17:17
Klaudia18: wychodzi mi że = −x2 cosx+2(xsinx−x(−cosx)) i po podstawieniu 0 wszystko jest zerem a jak
podstawię π to wychodzi mi że −π2(−2)(−1) w czym błąd ?
19 sty 17:18
Kejt:
przez części:
∫x2sinxdx=|u=x2, u'=2x; v'=sinx, v=−cosx|=−x2cosx+2∫xcosxdx=
|u=x, u'=1; v'=cosx v=sinx|=−x2cosx+2xsinx−2∫sinxdx=−x2cosx+2xsinx+2cosx+C
sprawdź teraz.
19 sty 17:18
Klaudia18: ok Kejt miałam tak samo ale wynik powinien być
π2−4
a mi nadal wychodzi z Twojego wyniku to samo, wiesz możę w czym błąd ?
19 sty 17:22
Klaudia18: przepraszam zrobiłam błąd w podstawieniu 0 tam wychodzi ze 2cos0 to 2
juz w porządku

19 sty 17:23
Kejt: tak.. w obliczeniach

[−π
2cosπ−0]+[2πsinπ−0]+[2cosπ−2cos0]=π
2+0−2−2=π
2−4

19 sty 17:27
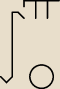 całka oznaczona właściwa.
∫ (0 do π)
∫x2 sinx dx =
mam mały problem z wynikiem powinno być π2 − 4
całka oznaczona właściwa.
∫ (0 do π)
∫x2 sinx dx =
mam mały problem z wynikiem powinno być π2 − 4

 [−π2cosπ−0]+[2πsinπ−0]+[2cosπ−2cos0]=π2+0−2−2=π2−4
[−π2cosπ−0]+[2πsinπ−0]+[2cosπ−2cos0]=π2+0−2−2=π2−4 