try
Radek:
Rozwiąż równanie w przedziale <0,2π>
4cos
2x−3=0
4cos
2x=3
| | √3 | | −√3 | |
cosx= |
| lub cosx= |
| |
| | 2 | | 2 | |
| | 5π | | 5π | | 5π | | 12π | | 7π | |
x= |
| lub x=− |
| +2π=− |
| + |
| = |
| |
| | 6 | | 6 | | 6 | | 6 | | 6 | |
| | π | | 5π | | 11π | |
W odp mam tylko x= |
| lub x= |
| lub x= |
| |
| | 6 | | 6 | | 6 | |
19 sty 16:32
Radek: ?
19 sty 16:53
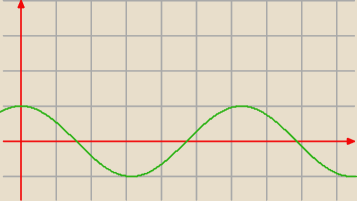
PW: Muszą być cztery rozwiązania − poprzyj to rysunkiem przebiegu f(x) = cosx na [0,2π].
19 sty 16:58
Radek:
19 sty 17:03
Ajtek:
Błąd w odpowiedziach i tyle.
19 sty 17:12
PW: Za dużo, tylko nad przedziałem [0,2π].
| | √3 | | √3 | |
Kreska y= |
| przecina wykres w 2 punktach, kreska y = − |
| też. |
| | 2 | | 2 | |
19 sty 17:14
Radek:
Dziękuję Panowie.
19 sty 17:31
