udowodnić, że sin^2x cos^2x = 1 Klaudia: Cześć Potrzebuje pomocy a raczej wyjaśnienia czy cos takiego da sie obliczyc i z czego mam skorzystać żeby to zrobic. mUsze udowodnić,że sin²x + cos²x = 1

	cosx
y=
	lnx

	lnx
y=
	2sinx

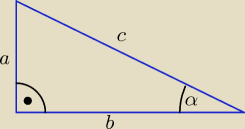
Bogdan: Wyprowadźmy wzór: sin²α + cos²α = 1 Z twierdzenia Pitagorasa: a² + b² = c² / : c²

	a		b
(		)2 + (		)2 = 1
	c		c

a		b
	= sinα,		= cosα
c		c

A o co chodzi z dwoma następnymi wyrażeniami ?

Klaudia: A te drugie to mam obliczyć pochodne, ale chtyba sobie z tym poradze napisze rozwiazanie tylko jakby ktos byl tak uprzejkmy i napisal czy dobrze

	cosx		−sinx * lnx− cosx* 1x
y=		=
	lnx		ln2x

	1x*2sinx−lnx*2cosx
y=
	2sin2x

A i dziekuje bardzo bardzo Bogdanowi za pomoc

AS: W ostatniej pochodnej w mianowniku winno być 4sin²x

Klaudia: tak faktycznie mas zrację dzięki