nierownosc Łukasz1:

	π		1
sin(3x−		)<		Nie potrafie robic nierownosci trygonometrycznych
	7		2

agus: sinα=¹₂ dla α=^π₆+2kπ oraz α=⁵₆π+2kπ Zatem sinα<¹₂ dla α∊(⁵₆π+2kπ,^π₆+2(k+1)π), k∊ℤ czyli ⁵₆π+2kπ < 3x−^π₇ < ^π₆+2(k+1)π, czyli masz dwie nierówności ⁵₆π+2kπ < 3x−^π₇ 3x−^π₇ < ^π₆+2(k+1)π z których musisz wyznaczyc przedziały dla x

Bogdan:

	π
α =
	7

Najpierw rozwiązujemy równanie:

	π		1		π		π
sin(3x −		) =		⇒ sin(3x −		) = sin
	7		2		7		6

	π		π		π		π
3x −		=		+ k*2π lub 3x −		= π −		+ k*2π k∊C
	7		6		7		6

	π		π		π		π
3x =		+		+ k*2π lub 3x =		+ π −		+ k*2π
	7		6		7		6

	13		1		41		1
3x =		π + k*2π / *		lub 3x =		π + k*2π / *
	42		3		42		3

	13		2		41		2
x =		π + k*		π lub x =		π + k*		π
	126		3		126		3

	2
Widzimy, że okres funkcji T =		π
	3

	13		41
Dla k = 0: x =		π lub x =		π
	126		126

	π		1
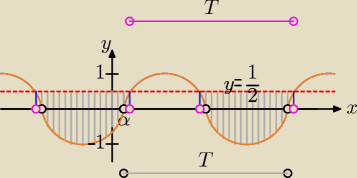
Teraz szkicujemy wykres funkcji y = sin(3x −		) oraz prostą y =		.
	7		2

Z wykresu i wykonanych obliczeń odczytujemy przedziały na osi x, w których sinusoida

	1
leży pod prostą y		y.
	2

	41		2		13
Wyznaczamy pierwszy przedział: (		π −		π;		π) =
	126		3		126

	43		13
= (−		;		π).
	126		126

	π		1
Odp.: sin(3x −		) <
	7		2

	43		2		13		2
dla x∊(−		+ k*		π;		π + k*		π).
	126		3		126		3