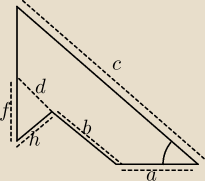
Pole figury (chyba nie takie proste jak by się wydawać mogło).. xsound: Hejka wszystkim ! Mam wielki problem. Muszę wyznaczyć z figury z obrazka wzór na jej pole.. Wszystko byłoby łatwo i w ogóle gdyby.. pewne rzeczy były równoległe, gdyby katy proste były w niej itp.. Bardzo proszę o zerknięcie, jeśli ktoś ma co mogłoby mnie naprowadzić.. z góry dzięki Rysunek nie najlepszy.. jakby coś mam w jpg dobra jakośc, tutaj tylko żeby przedstawić problematyke. Nie mam żadnych założen co do 'b' i 'c' czy są rownolegle, ale sprawdzałem w photoshopie, i nie są. 'd' jest przedłużeniem 'b' (na moim rysunku wyszlo ciut nierowno) a kąt na rysunku pomiedzy a i c to alfa. Czyli dane w zadaniu to dlugosci: a, b, c ,d ,h ,f oraz kąt alfa. Sporo tych danych i pewnie trzeba je wykorzystać. Ale szczerze mówiąc moje pomysły.. pokonczyly sie...

wredulus_pospolitus: to podeślij jpg'a

xsound: Proszę, tu jpg https://imagizer.imageshack.us/v2/566x466q90/802/zy49.jpg Próbowałem stworzyć 3 osobne figury, nawet 4 z tego. Np pole trójkąta 'h' , 'f' 'd' mozna ze wzorku, ale co do reszty nie mam pojecia. Planimetria − dobrze mówie ? − to chyba ten dział

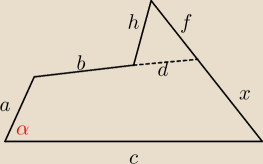
PW: fdh − znamy wszystkie boki, a więc obliczymy kąt między f i d, a w konsekwencji kąt β między d i przedłużeniem f (czwartym bokiem deltoidu, oznaczmy go e). Obliczenie przekątnej p deltoidu jest możliwe, bo mamy kąt i dwa boki a, c. Trójkąt o bokach e, (d+b) i p ma dane dwa boki i kąt β − da się wyliczyć bok e.

xsound: przedłużenie "f" ? nie wkradła się tam pomyłka ? przedłużając f nie otrzymujemy deltoidu

PW: To jest x na rysunku wredulusa. A "deltoid" to lapsus − powinno być "trapezoid" − po prostu czworokąt o bokach (d+b), a, c, e w moich oznaczeniach.

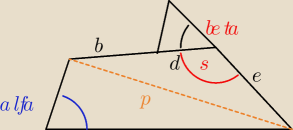
xsound: Chwila, przekątna 'p' ? masz na myśli taką (na rysunku przerywana linia) czerwone 'b" − to kąt beta., ten kat nie jest w "trapezoidie" , chyba ze wezmiemy 180−β = s wtedy mamy ten kąt trapezu ( kąt s − na czerwono na rysunku)

xsound: podbijam

PW: Podpowiedziałem wszystko co potrzeba. Chyba nie chcesz zrozumieć. Gotowej recepty na pole nie podam − to Ty masz kłopot.

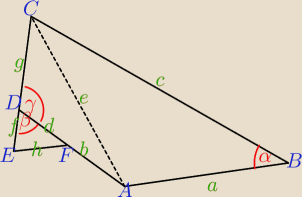
Bogdan: a może w ten sposób: cosγ = cos(180^o − β) = −cosβ Korzystamy z twierdzenia kosinusów. h² = d² + f² − 2df cosβ ⇒ cosβ = ... |AC|² = e² = a² + c² − 2ac cosα i e² = (b+d)² + g² − 2g(b+d) cosγ stąd g = ... Pole figury P = P_ABC + P_ACD + P_DEF =

	1		1		1
=		ac sinα +		g(b+d) sinγ +		df sinβ
	2		2		2

Można także stosować wzór Herona na pole trójkąta ABC i DEF

xsound: Dziękuje Bodgan ! Szczerze mówiąc pamiętam Cie tutaj z czasów mojej matury. Pomagałeś zawsze Pozdrawiam gorąco!

Bogdan:

xsound: Wstyd przyznać ale utknąłem przy czymś banalnym.. wyliczając "g" e² = (b+d)² + g² −2g(b+d)cosγ do postaci g(g−2(b+d)cosγ) = e² − (b+d)² I chyba to wyciegniecie "g" przed nawias nie jest najlepszym rozwiazaniem..

Bogdan: To jest przecież równanie kwadratowe z niewiadomą g: g² + 2g(b+d) cosγ + (b+d)² − e² = 0, oblicz Δ

xsound: uhm.. racja.. Δ = 4g² ( (b+d)²cos²γ − (b+d)² −e² ) )

Bogdan: g jest zmienną, Δ = 4(b+d)²cos²γ − 4(b+d)² + 4e² = ...

xsound: na tej podstawie można oszacować znak delty ? (zwykle takie zadania robiłem w oparciu o liczby, stad ten mętlik w głowie jeśli mam podane same litery. więc Δ =... = 4(b+d)² ( cos²γ − 1) + 4e² Zgadza się?

xsound: .. Δ = 4(b+d)² sin^γ + 4e² zakładając że krawedzie b, d, e są wieksze od 0, delta będzie większa od 0 więc mam liczyć g1,g2 ?

xsound: Czy jest jakiś sposób na unikniecie liczenia delty ? Wzór jest bardzo długi na te chwile, a program staje sie jeszcze bardziej skomplikowany...

xsound: Przepraszam za post pod postem. Mam wyliczone P_ΔDEF oraz P_ΔABC zgodnie z oznaczeniami z ostatniego rysunku Bogdana. Co do wzoru na ΔACD , czy możliwe jest wyprowadzenie wzoru jak najbardziej optymalnego ?

Bogdan: Dokończę moją ścieżkę prowadzącą do obliczenia pola trójkata ACD. Z twierdzenia kosinusów w trójkącie ABC: e² = a² + c² − 2ac cosα

	d2 + f2 − h2
Z twierdzenia kosinusów w trójkącie DEF: cosβ =
	2df

cosγ = −cosβ Z twierdzenia kosinusów w trójkącie ACD: e² = (b+d)² + g² − 2(b+d)g cosγ g² − 2(b+d)g cosγ + (b+d)² − e² = 0 Δ = 4(b+d)²cos²γ −4(b+d)² + 4e² = 4(b+d)²(cos²γ − 1) + 4e² = 4(e² − (b+d)²sin²γ) g = (b+d)cosγ + √e² − (b+d)²sin²γ

	1
Pole trójkąta ACD =		(b+d)g sinγ
	2

xsound: sinγ można wyliczyć z "1dynki tryg. ", prawda? znamy przeciez cosγ , tylko wtedy wzorek jeszcze dluzszy niz poprzednio

xsound: ale chwila... sinγ = sin(180 − β) = sin β :=> sinγ = sinβ −czy jest to możliwe ?

Bogdan: Tak, sinγ = sinβ

xsound: Dziękuje Bogdan raz jeszcze za czas i cierpliwość ! Zrobione