Wykaż że ania19: Wykaż, że w trójkącie prostokątnym suma przyprostokątnych jest równa sumie średnic okręgu wpisanego i opisanego.

bezendu: https://matematykaszkolna.pl/forum/232476.html

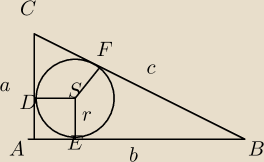
ICSP: Teza : a + b = 2r + 2R Zauważmy, że c = 2R. Wystarczy policzyć r. ΔEBS≡ΔSFB bo |SE| = |SF|, mają wspólny bok SB oraz ∡SEB = ∡SFB W identyczny sposób można pokazać przystawanie ΔDSC do ΔSFC Zatem z ΔEBS≡ΔSFB mamy równość : 1^o |EB| = |BF| oraz z ΔDSC do ΔSFC mamy : 2^o |AC| = |FC| dodając 1^o i 2^o stronami |EB| + |DC| = |BF| + |FC| a−r + b−r = c

	a + b − c
r =
	2

2R + 2r = 2c + a+b−c = a+b c.n.w.

PW: Średnica okręgu opisanego − wiadomo, przeciwprostokątna. Promień r okręgu wpisanego obliczymy z zależności

	ab
		= pr,
	2

która jest wynikiem policzenia pola prostokąta na dwa sposoby − z lewej strony wzór "tradycyjny", a z prawej wykorzystujący promień okręgu wpisanego (p oznacza połowę obwodu).

ICSP: bez 2 przy c na końcu

WAT: i zamiast |AC|=|FC| to |DC|=|FC|

ICSP: Faktycznie