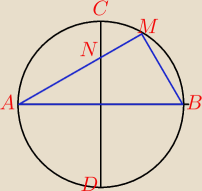
Zadanie na twierdzenie Gabaa: W okręgu o środku O poprowadzono dwie prostopadłe średnice AB i CD. Z punktu A poprowadzono cięciwę AM przecinającą średnicę CD w takim punkcie N, że w czworokąt OBMN można wpisać okrąg. Wykaż, że miara kąta ostrego BAM jest równa 30°. Proszę o pomoc

wredulus_pospolitus: masz wykazać że czworokąt można wpisać ... czy masz przyjąć że można ... więc masz wykazać że ∡BAM = 30^o

Gabaa: Tak, wykazać że ∡BAM wynosi 30°

wredulus_pospolitus: w czworokąt można wpisać czy go można opisać na okręgu

Gabaa: w czworokąt można wpisać okrąg