funkcje zadanie: Czy funkcja f :R→R okreslona wzorem f(x)=[x+a]−[x+b] jest ciagła, jezeli a) a=1/2, b=3/2 ....... b) a=1/3, b=−2/3 ....... c) a=1/4, b=3/4 ....... d) a=1/5, b=−9/5 ....... mam pytane mam narysowac te funkcje do kazdego podpunktu?

wredulus_pospolitus: a te [] oznacza co wartość bezwzględną czy też część całkowitą

zadanie: czesc calkowita

wredulus_pospolitus: oczywiście najlepiej by było, gdybyś narysował/−a ale możesz też sprawdzać podstawiając konkretne liczby lub spojrzeć chwileczkę na to co tam jest napisane

wredulus_pospolitus: zauważ, że:

	3		1
(a) b =		= 1 +		= 1 + a ... czyli [x+b] = [x+1+a] = 1 + [x+a]
	2		2

czy podobnie można zrobić w innych podpunktach w jakich a w tych w których nie można ... masz wskazówkę tak pokazać, że nie będzie ciągłości

zadanie:

	1		3
a gdybym chcial narysowac te funkcje np. z podpunktu a) czyli f(x)=[x+		]−[x+		] to w
	2		2

jaki sposob? gdybym mial rysowac osobno to zrobilbym tak:

	1
[x+		] − funkcje [x] przesunalbym o pol w lewo
	2

	3		3
[x+		] − funkcje [x] przesunalbym o		w lewo
	2		2

a jak mam odjac je od siebie to jak to narysowac?

wredulus_pospolitus:

	3		1
najlepiej zapisać to tak jak pisałem ... czyli [x+		] = 1+ [x+		} ... wtedy różnicę
	2		2

łatwo wyznaczasz możesz też po prostu narysować obie funkcje na jednej prostej i zauważyć 'schemat' pomiędzy nimi ... i odjąć

zadanie: dziekuje

Mila:

	1		1
a) f(x)=[x+		]−(1+[x+		])=−1 funkcja stała
	2		2

	1		1		1		1
b) f(x)=[x+		]−([x−1+		])=[x+		]−(−1+[x+		])=1
	3		3		3		3

c)f(x)= wg mnie nie jest ciągła d)f(x)=2 Arturze, sprawdź.

wredulus_pospolitus: dokładnie tak

Mila:

wredulus_pospolitus: (c) nie jest ciągła, wystarczy zauważyć: niech x=0.24(9) f(0,24(9) ) = 0 − 0 = 0 niech x=0,5 f(0,25) = 0 − 1 = −1

zadanie: a mam pytanie jak narysowac y={log₄x} jak to sprawdzic w wolframie? {x} − czesc ulamkowa

wredulus_pospolitus: log_ax ... wygląda (kształt) tak samo dla każdego a>1 więc log₄x rysujesz jak lnx jak chcesz w wolfim to piszesz: PLOT[LOG[4,x]] pamiętaj tylko aby na wykresie zaznaczyć: real−valued plot

zadanie: http://www.wolframalpha.com/input/?i=PLOT%5BLOG%5B4%2Cx%5D%5D to ten? bo ja chce w czesci ulamkowej

zadanie: ?

zadanie: ?

zadanie: jak obliczyc taka granice

	log2(n+8)
lim		?
	log2n

n→∞

Mila: y=log[4,x]−floor(log[4,x])

zadanie: dziekuje a jaki wzor zastosowac aby obliczyc te granice z logarytmem?

zadanie: ?

Mila: Może o trzech ciągach, z lewej

log2(n)
	a z prawej teraz nie wiem.
log2(n)

zadanie:

	log2(2n)		log22+log2n
a z prawej moze byc tak:		=		=
	log2n		log2n

	1+log2n		log2n(1+1log2n)
=		=		=1 ?
	log2n		log2n

zadanie: pytalem o narysowanie funkcji y={log₄x} bo musze obliczyc granice : lim{log₄x} x→16⁻ oraz x→16⁺ odp. to 1 oraz 0 rowniez mam taka granice lim{log₈x} x→16⁻ oraz x→16⁺

	1		1
od[. to		oraz
	3		3

jak do tego dojsc?

Mila: 2n>n+8 dla n>8, więc myślę,że może być, licznik zwiększyłeś.

zadanie: dziekuje

zadanie: a to zadanie z godziny 22:46 ? jak narysowac takie funkcje ?

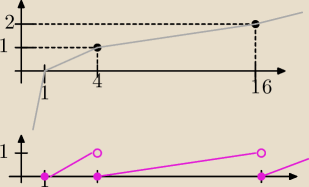
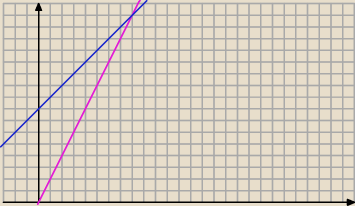
zadanie: pierwszy wykres to wykres y=log₄x drugi wykres to wykres y={log₄x} dobrze?

zadanie: ?

zadanie: ?

Mila: Dobrze, ale wieczorem wrócę do tego. Najgorszy jest przedział (0,1), tam maleńkie ukośne odcinki. obierz dużą jednostke i narysuj np. dwa przedziały dla log₂x, bedzie łatwiej.