Prawdopodobieństwo - zmienne losowe
Gustlik: Mam takie zadanko z prawdopodobieństwa:
Wyznacz funkcję prawdopodobieństwa oraz wartość oczekiwaną i wariancję zmiennej losowej
Z=2(Y−X), gdzie X i Y są zmiennymi o rozkładach:
xi −1 2
pi 3/5 2/5
yi 4 1
pi 1/3 2/3
Zmienną Z wiem, jak obliczyć, np. Z1=2(Y1−X1)=2(4−(−1))=2*5=10, tylko jak obliczyć
prawdopodobieństwo zmiennej np. Z1, jeżeli prawdopodobieństwa zmiennych X1 i Y1 są różne?
Mogę prosić o jakieś wskazówki, bo dawno nie robiłem takich zadań. Z góry dzięki.
18 sty 00:08
wredulus_pospolitus:
P(Z
1) = P(X
1)*P(Y
1)
P(Z
2) = P(X
1)*P(Y
2)
P(Z
3) = P(X
2)*P(Y
1)
P(Z
4) = P(X
2)*P(Y
2)
P(Z
1) + P(Z
2) + P(Z
3) + P(Z
4) =
| | 3 | | 1 | | 3 | | 2 | | 2 | | 1 | | 2 | | 2 | |
= |
| * |
| + |
| * |
| + |
| * |
| + |
| * |
| = |
| | 5 | | 3 | | 5 | | 3 | | 5 | | 3 | | 5 | | 3 | |
| | 1 | | 2 | | 2 | | 4 | | 3+6+2+4 | |
= |
| + |
| + |
| + |
| = |
| = 1 |
| | 5 | | 5 | | 15 | | 15 | | 15 | |
więc jest dobrze
18 sty 00:51
wredulus_pospolitus:
w końcu aby zmienna losowa Z przyjęła wartość Z1 ... to musi zajść X = X1 i Y = Y1 ... i
stąd mnożymy odpowiednie prawdopodobieństwa
18 sty 00:52
asdf: nie wiem czy dobrze, ale:
EZ = E(2(Y−X)) = 2E(Y−X) = 2(EX − EY)
gdzie:
EX = −1*3/5 + 4/5
EY = 4/3 + 2/3
dla wariancji, tylko warunkow nie mam zapisanych
D
2(X±Y) = D
2X + D
2Y ± 2cov(X,Y)
cov(X,Y) = E(X*Y) − EX * EY
E(X*Y) = ∑x
i*y
j * p
ij
18 sty 00:55
asdf: wredulus, moglbys sprawdzic?
18 sty 00:57
wredulus_pospolitus:
asdf ... ale po co się tak bawić ... zmienna losowa Z ma rozkład punktowy ... znamy punkty ...
znamy prawdopodobieństwa, po co do tego mieszać X i Y przy wyliczaniu EZ i D
2Z
| | 1 | | 9 | | 18 | | 3 | |
EZ wyszedł Ci: EZ = 2*(2− |
| ) = 2* |
| = |
| = 3 |
| |
| | 5 | | 5 | | 5 | | 5 | |
| | 1 | | 2 | | 2 | | 4 | |
a jakby na piechotę liczyć EZ = |
| *10 + |
| *4 + |
| *4 + |
| *(−1) = |
| | 5 | | 5 | | 15 | | 15 | |
| | 3 | | 8 | | 4 | | 3 | |
= 2 + 1 |
| + |
| − |
| > 3 |
| |
| | 5 | | 15 | | 15 | | 5 | |
więc coś nie tak jest wyliczone
18 sty 01:07
wredulus_pospolitus:
dobra ... znalazłem swój błąd ... nie ma być (−1) tylko (−
2)
18 sty 01:08
Trivial:
A co ze starą dobrą zasadą liniowości?
| | 3 | | 2 | | 1 | |
E[X] = (−1)* |
| + 2* |
| = |
| |
| | 5 | | 5 | | 5 | |
| | 1 | | 2 | |
E[Y] = 4* |
| + 1* |
| = 2 |
| | 3 | | 3 | |
| | 1 | | 18 | |
E[Z] = E[2(Y−X)] = 2*(E[Y] − E[X]) = 2*(2 − |
| ) = |
| |
| | 5 | | 5 | |
18 sty 01:12
asdf: ja tylko wzorki podrzuciłem i chciałem spytać czy dobrze
18 sty 01:12
Trivial: Aha, już wiem co...
asdf już to zauważył.
18 sty 01:13
18 sty 01:16
Trivial:
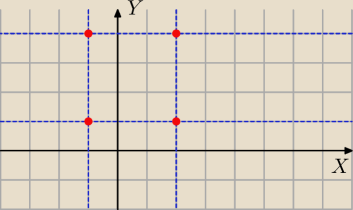
Jako że zmienne są niezależne, przestrzeń zdarzeń można traktować jako każdą parę (X,Y). I już
wszystko jasne.
f(x,y) = f
X(x)*f
Y(y)
18 sty 01:16
Gustlik: Dzięki
18 sty 23:40