Extrema lokalne Janek: Witam ! Mam takie zadanie: Wyznacz extrema lokalne funkcji 2/x * ln(x/2) Mógłby mi ktoś pomóc.

Kejt: pochodna policzona?

Janek: no własnie wyszła mi: −2/(x²)* (ln(x/2) +1) i nie jestem pewien czy to dobry wynik

Kejt: wyszło mi tak samo no to teraz wyznacz przedziały kiedy ta pochodna jest <0, =0 i >0

asdf: http://www.wolframalpha.com/input/?i=%28+2%2Fx+*+log%5Be%2C+x%2F2%5D+%29+%27+%3D+-2%2Fx%5E2+*+%28log%5Be%2Cx%2F2%5D+%2B+1+%29 false

Kejt: poprawka.. jednak jest drobny błąd.

	x
liczyłeś pochodną też z		?
	2

Janek: no liczyłem i wyszła mi taka pochodna i jedno miejsce zerowe x=e/2. Wiem jak postepować w tym zdaniu ale nie wiew czy mi wszystko dobrze wyszło.

Kejt: oki, to skończę swoje zadanko i policzę Twoje.. potem porównamy

Janek: będę bardzo wdzięczny

asdf: http://www.elektroda.pl/rtvforum/topic1861886.html http://www.wolframalpha.com/input/?i=max%7Bf%28x%29+%3D+%28+2%2Fx+*+log%5Be%2C+x%2F2%5D+%29+%7D

Janek: Wszystko okej tylko to mi nic nie daje bo nie wiem jak niby ta pochodna ma byc policzona zeby tak wyszło. LICZE: (2/x)' * ln(x/2) + [ln(x/2]' *2/x

Janek: dobra juz wiem gdzie miałem błąd. Teraz tez wyszło mi x=2e

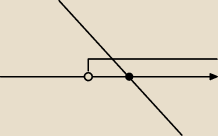
Janek: Tak powinien wyglądać wykres pochodnej z uwzględniona dziedzina czy prosta powinna być poprowadzona z góry?

asdf: Naucz sie korzystac z wolframa On sie nigdy nie myli, a jak ktos powie, ze "wolfram sie czasem myli" (patrz: moj dawny prowadzacy) to jest juz przeslanka, zeby udowodnic głupstwo, jakie powiedziala ta osoba

asdf: tak, ta pochodna jest malejąca

asfas: Oj asdf, asdf jak będziesz tak ślepo wierzył wolframowi to życzę powodzenia ...