tr
Radek:
kolejne równanie i kolejny problem.
Rozwiąż równanie 2cosx−sin2x=1−sinx
2cosx−sin2x=1−sinx
2cosx−2sinxcosx−1+sinx=0
2cosx(1−sinx)−(1−sinx)=0
(1−sinx)(2cosx−1)=0
17 sty 17:23
Radek:
Oczywiście w przedziale <0,2π>
17 sty 17:24
PW: | | 1 | |
cosx = |
| ma dwa rozwiązania w [0, 2π) |
| | 2 | |
17 sty 17:26
Bizon:
... to nie wszystkie −

17 sty 17:28
Radek: Właśnie mam problem ze znalezieniem wszystkich
17 sty 17:31
Mila:
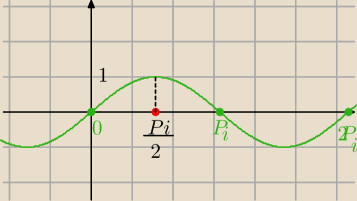
1) musisz wiedzieć jak przebiega wykres funkcji y=sinx
a) y=sinx
sinx=0
x=0+kπ, k∊C
W przedziale <0,2π> masz 3 rozwiązania: {0,π,2π}
b) sinx=1
W przedziale <0,2π>
17 sty 17:41
Radek:
ale mi chodzi o cosx
17 sty 17:48
Mila:
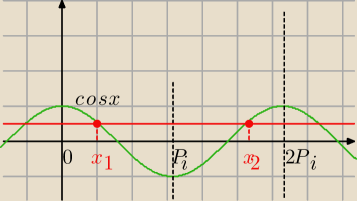
I) sposób
| | π | | π | | 5π | |
x= |
| lub x=2π− |
| = |
| |
| | 3 | | 3 | | 3 | |
to są rozwiązania z przedziału <0,2π>
| | π | | π | |
x= |
| ∊ <0,2π> lub x=− |
| nie należy , ale jest to funkcja okresowa |
| | 3 | | 3 | |
| | π | |
i rozwiązanie zapisujemy: x=− |
| +2kπ |
| | 3 | |
| | −π | | 5π | |
dla k=1 mamy x= |
| +2π= |
| ∊<0,2π> |
| | 3 | | 3 | |
17 sty 17:51
Radek:
czyli od jesli mam rozwiązanie ujemne to 2π− ? zawsze tak ?
17 sty 18:00
Mila:
Korzystasz z wzoru redukcyjnego:
cosα=cos(360−α)
17 sty 18:19
Radek:
To a dla sin też tak wygląda rozwiązanie ?
Mam już wyniki tych matur.
17 sty 18:23
Mila:
Dla sinusa inaczej, zobacz na wykres.
To jaki masz wynik maturki?
17 sty 18:28
Radek: dla sin π−coś ?
P 86 R 76
17 sty 18:30
matyk: nieźle
17 sty 18:39
Mila:
Gratulacje, to bardzo dobry wynik.

Jak wypadło w klasie?
| | π | | π | |
x= |
| +2kπ lub x=π− |
| +2kπ |
| | 6 | | 6 | |
17 sty 18:49
Radek:
Z podstawy 3 miejsce bo dwa pierwsze to 100% a R w wynik
17 sty 18:53
Mila:
Chodzi mi o to jak napisała klasa, jaki jest poziom klasy.
17 sty 19:31
Radek:
Większość w przedziale 80−84 P. A R różnie dwie osoby po 100% reszta 60−80
17 sty 19:34
Mila:
To jesteś w dobrej klasie.
17 sty 19:38
Radek:
Tylko, że 3/4 chodzi na prywatne lekcje matematyki, a ja szukam pomocy na forum.
17 sty 19:39
asdf: oj Radek Radek

Szczerze, to pomoc na forum jest duzo lepsza niz prywatne lekcje

Na
prawdę! 2 lata temu zaczynałem studia...napisalem mature ~80% (podstawe, rozszerzenie mnie nie
interesowalo − mialem egzamin zawodowy). Koncząc kurs analizy i algebry zdałem (według mnie) z
bardzo satysfakcjonującym wynikiem, a to dzięki forum

17 sty 19:44
Radek: Tylko ja mam takie wrażenie, że nie dam rsdy przerobić wszystkich zadań i w maju będzie klapa.
Z podstawa sobie poradzę ale z R nie rozumiem połowy zadań.
17 sty 19:46
asdf: osoby majace prywatne lekcje − moze mają łatwiej do zrozumienia tematu, ale jezeli chcesz isc
na studia jest to bardzo dobry sposob na oswojenie się z "akademickim nauczaniem", tzn.
pojdziesz na wyklad, dostaniesz wskazowki, literature i pracuj sam...wykształciuchy po
prywatnych lekcjach będą mieli zderzenie ze ścianą, Ty natomiast będziesz już potrafił radzić
sobie...uczysz się samodzielności w taki sposób

17 sty 19:47
asdf: "przerobic wszystkich zadan" − nie popadaj w paranoje...z matury musisz miec 100%? NIE! jak
napiszesz na 90% cos sie stanie? − tez nie...rob tyle ile potrafisz, zebys Ty sam do siebie
nie mial po napisaniu egzaminu pretensji o to, ze sie nie przylozyles do tego

Każdy ma
swoje miejsce w szeregu, jak bedziesz nad sobą pracowac to osiagniesz sukces

17 sty 19:51
Mila:
Jeśli R napiszesz na 50% to też będzie dobrze, pracuj − będzie dobrze, w końcu coraz lepiej
rozwiązujesz zadania.
17 sty 19:56
Radek: 50% to zamyka zdecydowanie drogę na to co chcę iść. Ale będę robił co w mojej mocy.
17 sty 19:59
asdf: i słuchaj się Mili, Basii i innych osób! Daje swoje slowo, ze bedzie dobrze!

P.S Sam korzystalem to wiem! (teraz juz moze mniej, bo czym innym się zajmuje niz czystą
matematyką)
17 sty 20:02
Mila:
Zadanie dla Radka.
Rozwiąż równanie:
4cos2x=4sinx+1
17 sty 20:21
Radek:
4cos
2x=4sinx+1
4cos
2x−4sinx−1=0
4(1−sin
2x)−4sinx−1=0
t=sinx t∊<−1,1>
−4t
2−4t+3=0 /(−1)
4t
2−4t−3=0
Δ=64
√Δ=8
| | π | | π | | 7π | |
x=− |
| +2kπ lub x=π+ |
| = |
| +2kπ |
| | 6 | | 6 | | 6 | |
17 sty 20:36
Mila:
Pomyłka w równaniu kwadratowym,
4t2+4t−3=0
17 sty 21:01
Radek: A wynik poprawny ?
17 sty 21:01
Mila:
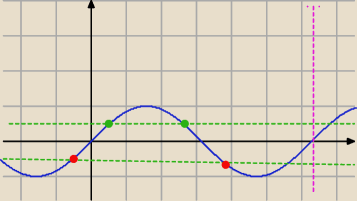
Rozwiązanie równania
17 sty 21:10
Radek: Może mi Pani jeszcze kilka przykładów dać ?
17 sty 21:11
Mila:
2) 2cos2x−5sinx=4 dla x∊<0,2π>
17 sty 21:24
Mila:
3) 2sin2x−2sin2x*cosx=1−cosx dla x∊<0,2π>
to są równania z matur.
17 sty 21:29
Radek:
2cos
2x−5sinx=4
2cos
2−5sinx−4=0
2(1−sin
2x)−5sinx−4=0
2−2sin
2x−5sinx−4=0
−2sin
2x−5sinx−2=0 /(−1)
2sin
2x+5sinx+2=0
sinx=t t∊<−1,1>
2t
2+5t+2=0
Δ=9
√Δ=3
ok ?
17 sty 21:39
Radek:
2sin2x−2sin2x*cosx=1−cosx dla x∊<0,2π>
4sinxcosx−4sinxcos2x+cosx−1=0
4sinxcosx(1−cosx)−(1−cosx)=0
(1−cosx)(4sinxcosx−1)=0
i tutaj problem z drugim nawiasem
17 sty 21:44
Mila:
| | π | |
x=− |
| ∉<0,2π>, to dodamy 2π |
| | 6 | |
| | 7π | | π | | 11π | |
x1= |
| lub x2=− |
| +2π = |
| |
| | 6 | | 6 | | 6 | |
17 sty 21:45
Radek: Dziękuję a ten drugi podpowie Pani ?
17 sty 21:47
Mila:
(1−cosx)=0 lub (4sinxcosx−1)=0
w 3 równaniu jednak zmieniłeś sin2x na sin2x
17 sty 21:48
Radek:
cosx=1
x=kπ lub x=2π ?
17 sty 21:49
Mila:
17:51 wykres, zobacz. Popraw 21:49.
17 sty 21:53
Radek:
x=0 lub x=2π
?
17 sty 21:55
Mila: Tak.
Drugie :
(4sinxcosx−1)=0⇔
2*2sinxcox=1
dokończ
17 sty 21:57
Radek:
Ale jak Pani zwinęła to mam teraz:
17 sty 21:59
asdf:
sin(2x) = 2sinxcosx
przekształcenie:
można pokusić się o próbę rozwiązania w pamięci

17 sty 22:00
Radek: ?
17 sty 22:02
asdf: da sie to "po nie szkolnemu" :
| | 1 | | π | |
zobacz, ze sin(x) = |
| , to x = |
| |
| | 2 | | 6 | |
więc dla:
| | 1 | | π | | π | |
sin(2x) = |
| , to 2x = |
| ⇒ x = |
| |
| | 2 | | 6 | | 12 | |
17 sty 22:19
asdf: tu nie zapomnij o okresowości ... nie chce mi sie juz jej analizować bo to trywialne juz jest
17 sty 22:20
asdf: z wykorzystaniej funkcji cyklometrycznych (to nie jest nic skomplikowanego), zobacz i
przeanalizuj chociaż:
| | 1 | | 1 | |
sin(x) = |
| ⇒ arcsin( |
| ) = x |
| | 2 | | 2 | |
tutaj masz takie coś:
17 sty 22:22
asdf: w zwyklych funkcjach trygonometrycznych chodzi o to, ze dajesz kąt, a otrzymujesz wartość,
natomiast w funkcjach cyklometrycznych dajesz wartość, a otrzymujesz kąt

17 sty 22:24
Radek:
Wolę to zrozumieć po szkolnemu
17 sty 22:24
Mila:
| | π | | 5 | |
2x= |
| +2kπ lub x= |
| π+2kπ⇔ |
| | 6 | | 6 | |
| | π | | 5π | |
x= |
| +kπ lub x= |
| +kπ |
| | 12 | | 12 | |
i teraz sprawdzaj czy dla k=1 rozwiązania należą do <0,2π>
17 sty 22:31
Radek:
należą
17 sty 22:32
asdf: a co jest w tym skomplikowanego ? Nie wiem czemu, ale licealiści zawsze maja problem, można
powiedzieć traume ... boją się rozwiązywać zadania "normalnie", tzn. po swojemu − niekiedy
sposoby rozwiazywania zadan w szkole są tak tragicznie rozwiazywane, ze glowa boli...mozna to
zrobic 3 razy szybciej i 10 razy mniej te rozwiazanie skomplikowac. Moze jeszcze nie wiesz,
ale zadania na maturze (oh tak, ten okropnie prosty egzamin, ktorego wiekszosc sie boi) mozna
rozwiazywac PO SWOJEMU, byle byla w tym wszystkim LOGIKA! W szkole nie tlumaczą...w szkole
uczą schematów rozwiazywania zadania i to jest przykre

jak ostatnio udzielalem korków z matmy mial duzy problem z rozwiazaniem takiego zadania:
Znajdź argument funkcji, dla którego funkcja przecina oś odciętych:
y(p) = p
2 − 3,
Nie wiedzial jak się za to zabrać, bo:
1. nauczyli go, że się pisze f(x), a nie "jakies "y(p)" (z zarzutami, ze nie ma czegos takiego)
2. nie wiedzial co to oś odciętych
drugie zadanie:
f(δ) = πlog
2(x)
pytanie:
podstawiając za argument funkcji wartość 1 odpowiedz na pytanie czy przecina oś odciętych
P.S Mógłbyś rozwiązać te zadania?

17 sty 22:33
Radek:
p=√3 lub p=−√3
17 sty 22:35
Radek:
Dziękuję Pani Milu już mi się rozjaśniło jak to rozwiązywać
17 sty 22:40
asdf: a drugie?
17 sty 22:40
Mila:
Teraz Radek wróć do zadania:
2sin2x−2sin2x*cosx=1−cosx dla x∊<0,2π>
I podaj wszystkie rozwiązania w podanym przedziale.
17 sty 22:42
Radek:
| | π | | 5π | |
x=0 x=2π x= |
| x= |
| |
| | 12 | | 12 | |
17 sty 22:43
Mila:
6 rozwiązan, dwa pierwsze zgadzają się.
17 sty 22:48
Radek: 6 ?
17 sty 22:49
Radek: ?
18 sty 16:27
ZKS:
W równaniu którym podała Mila i przedziale do jakiego należy x mamy 6 rozwiązań.
18 sty 16:45
Radek: ale jak je wyznaczyc ?
18 sty 20:11
Radek: ?
18 sty 20:48
Mila:
Napisz jak rozwiązywałeś równanie, wszystkie zapisy.
18 sty 20:53
Mila:
3) 2sin2x−2sin2x*cosx=1−cosx dla x∊<0,2π>
18 sty 20:55
Radek:
2sin
2x−2sin
2xcosx=1−cosx
2sin
2x−2sin
2xcosx−cosx−1=0
2sin
2x(1−cosx)+(cosx−1)=0
cosx=1 2six
2x=1
x=0 x=2π
2sin
2x=1
| | √2 | |
sinx=U{√2{2} lub sinx=− |
| |
| | 2 | |
| | 5π | |
x= |
| i dalej nie wiem ? |
| | 4 | |
18 sty 20:58
Mila:
Masz tam jeden błąd , rozwiązania (x) mają być dodatnie.
2sin
2x−2sin
2x*cosx=1−cosx i x∊<0,2π>
2sin
2x−2sin
2xcosx+cosx−1=0
2sin
2x(1−cosx)+(cosx−1)=0
2sin
2x(1−cosx)−(1−cosx)=0
(1−cosx)(2sin
2x−1)=0⇔
1−cosx=0 lub 2sin
2x−1=0⇔
| | √2 | | √2 | |
x=kπ lub sinx= |
| lub x=− |
| |
| | 2 | | 2 | |
| | π | | 3π | | 5π | | 7π | |
x=0 lub x=2π lub x= |
| lub x= |
| lub x= |
| lub x= |
| |
| | 4 | | 4 | | 4 | | 4 | |
18 sty 21:23
Radek:
Dziękuję, juz chyba w końcu zrozumiałem, teraz biorę się za inne zadania.
18 sty 21:25

 1) musisz wiedzieć jak przebiega wykres funkcji y=sinx
a) y=sinx
sinx=0
x=0+kπ, k∊C
W przedziale <0,2π> masz 3 rozwiązania: {0,π,2π}
b) sinx=1
1) musisz wiedzieć jak przebiega wykres funkcji y=sinx
a) y=sinx
sinx=0
x=0+kπ, k∊C
W przedziale <0,2π> masz 3 rozwiązania: {0,π,2π}
b) sinx=1
 I) sposób
I) sposób
 Jak wypadło w klasie?
Jak wypadło w klasie?
 Szczerze, to pomoc na forum jest duzo lepsza niz prywatne lekcje
Szczerze, to pomoc na forum jest duzo lepsza niz prywatne lekcje  Na
prawdę! 2 lata temu zaczynałem studia...napisalem mature ~80% (podstawe, rozszerzenie mnie nie
interesowalo − mialem egzamin zawodowy). Koncząc kurs analizy i algebry zdałem (według mnie) z
bardzo satysfakcjonującym wynikiem, a to dzięki forum
Na
prawdę! 2 lata temu zaczynałem studia...napisalem mature ~80% (podstawe, rozszerzenie mnie nie
interesowalo − mialem egzamin zawodowy). Koncząc kurs analizy i algebry zdałem (według mnie) z
bardzo satysfakcjonującym wynikiem, a to dzięki forum 

 Każdy ma
swoje miejsce w szeregu, jak bedziesz nad sobą pracowac to osiagniesz sukces
Każdy ma
swoje miejsce w szeregu, jak bedziesz nad sobą pracowac to osiagniesz sukces 
 P.S Sam korzystalem to wiem! (teraz juz moze mniej, bo czym innym się zajmuje niz czystą
matematyką)
P.S Sam korzystalem to wiem! (teraz juz moze mniej, bo czym innym się zajmuje niz czystą
matematyką)
 Rozwiązanie równania
Rozwiązanie równania


 jak ostatnio udzielalem korków z matmy mial duzy problem z rozwiazaniem takiego zadania:
Znajdź argument funkcji, dla którego funkcja przecina oś odciętych:
y(p) = p2 − 3,
Nie wiedzial jak się za to zabrać, bo:
1. nauczyli go, że się pisze f(x), a nie "jakies "y(p)" (z zarzutami, ze nie ma czegos takiego)
2. nie wiedzial co to oś odciętych
drugie zadanie:
f(δ) = πlog2(x)
pytanie:
podstawiając za argument funkcji wartość 1 odpowiedz na pytanie czy przecina oś odciętych
P.S Mógłbyś rozwiązać te zadania?
jak ostatnio udzielalem korków z matmy mial duzy problem z rozwiazaniem takiego zadania:
Znajdź argument funkcji, dla którego funkcja przecina oś odciętych:
y(p) = p2 − 3,
Nie wiedzial jak się za to zabrać, bo:
1. nauczyli go, że się pisze f(x), a nie "jakies "y(p)" (z zarzutami, ze nie ma czegos takiego)
2. nie wiedzial co to oś odciętych
drugie zadanie:
f(δ) = πlog2(x)
pytanie:
podstawiając za argument funkcji wartość 1 odpowiedz na pytanie czy przecina oś odciętych
P.S Mógłbyś rozwiązać te zadania? 