nierówność wielominów beata: Rozwiąż nierówność

9x2 − x4
	> 0
9−6x2 + x4

Darth Mazut: WSKAZÓWKA: Pomnóż obie strony nierówności przez wyrażenie w mianowniku podniesione do kwadratu

kika: (3x+x²)(3x−x²)((3−x²)²>0 i dalej dasz radę

beata: Robiłam i podstawiałąm niewiadomą pomocniczą t= x², ale nadal nie mogę z tym sobie poradzić.

Aga1.: Dalsze wskazówki Mianownik x⁴−6x²+9=(x²−3)²=[(x−√3)(x+√3)]²=(x−√3)²(x+√3)² licznik 9x²−x⁴=−x²(x²−9)=−x²(x−3)(x+3)

kika: 9−6t+t² Δ=0 t₁=t₂=3

Darth Mazut: 9x² − x⁴ = (3x+x²)(3x−x²) x⁴ − 6x² + 9 = (x² − 3)²

Mila:

9x2−x4
	>0
9−6x2+x4

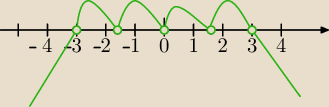
Z. x⁴−6x²+9≠0⇔ (x²−3)²≠0⇔x≠√3 i x≠−√3 Zamiast badać znak ilorazu badam znak iloczynu (9x²−x⁴)(9−6x²+x⁴)>0⇔ x²(9−x²)*(x²−3)²>0 i x≠√3 i x≠−√3⇔ x²*(3−x)*(3+x)>0 x=0 pierwiastek podwójny, x=3, x=−3 x∊(−3,3)\{−√3,0,√3}