hej zoffia: Co to oznacza ,że parabole są przystające ? mam podane miejsca zerowe funkcji i to , że jest przystająca do y=5x² i mam wyznaczyć wzór funkcji . Poproszę o wskazówki

Patronus: Wydaje mi się że to może oznaczać że współczynnik kierunkowy jest taki sam, czyli w nowej paraboli będzie: f(x) = 5x² + bx + c Podstaw miejsca zerowe i masz odp

zoffia: Mi się wydaje ,że jak są przystające to " stykaja się " wierzchołkami , czyli może współczynnik a będzie miał przeciwny znak? czyli −5x²...

J: Nigdy nie słyszałem prawdę mówiąc o "przystawaniu paraboli"

Patronus: to już prędzej styczne by napisali..., nie wiem

zoffia: kurcze , wie ktoś

kika: przystajaca to tak jak w geom to taka którą można przez przekształcenia nałozyć na siebie. Czyli dla 5x² będzie 5x²+4 5x²−4 5(x−2)²

Rafał28: Parabole jako figury geometryczne są przystające, gdy przy x² mają taki sam współczynnik. Ogólnie figury są do siebie przystające, gdy istnieje izometria przekształcająca jedną figurę w drugą.

Aga1.: W translacji o wektor, w symetrii osiowej, w symetrii środkowej otrzymujemy parabolę przystającą do danej ( zmienia się jedynie położenie), można wykorzystać szablon. np, y=5x2, y=−5x2 , y=5(x−1)²+7 , wykresy tych funkcji są parabolami przystającymi

Patronus: Czyli intuicyjnie dobrze zrozumiałem

kika: Intuicja nie zawiodła!

zoffia: ok , dzięki wielkie

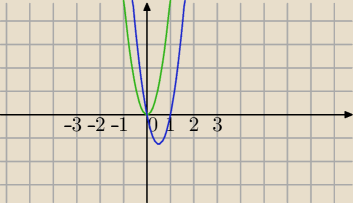
Mila: Parabola będzie przystająca po przesunięciu wykresu y=5x² o odpowiedni wektor, aby otrzymać podane miejsca zerowe. np. x₁=0 x₂=1

	1
xw=
	2

y=5x*(x−1) postać iloczynowa⇔y=5x²−5x

	1
xw=
	2

	5
yw=−
	4

	1		−1
y=5x2→T[		,		]→y=5x2−5x
	2		4

Sposób Patronusa szybszy, ale wytłumaczyłam przystawanie.