. Piotr 10: Liczby x₁, x₂ są pierwiastkami równania x²+x+A=0, a liczby x₃, x₄ są pierwiastkami równania x²+4x+B=0. Wiadomo, że (x₁,x₂,x₃,x₄) jest ciągiem geometrycznym o wyrazach całkowitych, Wyznacz A i B. Moje rozwiązanie, które zgadza się z odpowiedzią, lecz mam pewne wątpliwości, bo w kluczu jest inaczej rozwiązane i są założenia: 1⁰ x²+x+A=0 ; 2⁰ x²+4x+B=0 x₁=a₁ x₂=a₁*q x₃=a₁*q² x₄=a₁*q³ 1⁰ x₁+x₂=−1 a₁+a₁*q=−1 2⁰ x₃+x₄=−4 a₁*q²+a₁*q³=−4 a₁+a_q*q=−1 a₁*q²+a₁*q³=−4 a₁(1+q)=−1 a₁(q²+q³)=−4

1+q		1
	=
q2+q3		4

q³+q²−4q−4=0 q²(q+1)−4(q+1)=0 (q+1)(q²−4)=0 q=−1 v q=2 v q=−2 Dla q=−1, mam a₁ − a₁=−1 , 0=−1 sprzeczność

	1
Dla q=2, mam a1=−		∉, bo x1,x2,x3,x4 ∊C
	3

Dla q=−2 , mam a₁=1∊ Wtedy x₁=1, x₂=−2, x₃=4, x₄=−8 Ze wzorów Viete'a x₁*x₂=A A=−2 x₃*x₄=B B=−32 A na stronie 14 z tego linku http://www.tomaszgrebski.pl/arkusze/PAZDRO/2008%20PR%20z%20odp.pdf , jest troszkę inaczej rozwiązane I pytanie czy moje rozwiązanie jest w porządku ?

Maslanek: Założenia: Na początku pierwiastki muszą w ogóle istnieć, więc Δ≥0 (w razie gdyby q=1) Dodatkowo przy a₁(q²+q³)=−4 mamy q≠0 (oczywiste bo iloczyn dwóch liczb ma być rózny od zera

Piotr 10: Eh ok, czyli po punkcie już. A i jeszcze jedno. Jak mam zadanie z ostrosłupem lub z graniastosłupem to zawsze mam rysować rysunek ? Bo zrobiłem zadanie bez rysunku, bo nie był mi do niczego potrzebny, a patrzę w kluczu a tu dają 1 punkt za wykonanie rysunku i oznaczeniu tam danych

Maslanek: Nie wiem jak to wygląda, ale jeśli jest to mile widziane, to czemu nie

Piotr 10: Popatrz w tym linku strona 15. Nic w poleceniu nie było mowy o rysunku ,a jednak dali za to punkt. By mogli przynajmniej w poleceniu podać ''Wykonaj rysunek''

5-latek: Mnie uczyl moj mauczyciel od matematyki ze jesli mam zadanie z geometrii czy geometrii analitycznej ze zawsze mam robic rysunek chocby byl najprostszy

matyk: Za rysunek nie powinno być osobnego punktu jeśli nie ma w poleceniu aby go narysować. tak uczy dydaktyka.

Mila: Gdybyś w równaniu: a1(q²+q³)=−4 wyłączył q² to byłoby: a₁*q²(1+q)=−4 wtedy przed podzieleniem− założenia, tam w kluczu jest punkt za stosowne założenia, jedno dałeś, potem napisałeś ,że sprzeczność dla q=−1, nie powinieneś stracić punktu.

Mila: Zadanie dla Piotra narysuj wykres funkcji:

	sin2x−|sinx|
f(x)=		dla x∊(0,π)∪(π,2π)
	sinx

Mila: 3) 2sin²x−2sin²x*cosx=1−cosx dla x∊<0,2π> to są równania z matur.

Mila: 2) 2cos²x−5sinx=4 dla x∊<0,2π>

bezendu: Te zadania są do zrobienia ?

Mila: Tak, są wybrane z matur.

bezendu: 2cos²x−5sinx=4 2(1−sin²x)−5sinx−4=0 2−2sin²x−5sinx−4=0 2sin²x+5sinx+2=0 2t²+5t+2=0 t=sinx t∊<−1,1> Δ=9 √Δ=3 t₁=−2∉<−1,1>

	1
t2=−
	2

	1
sinx=−
	2

	7π		11π
x=		lub x=
	6		6

Mila: Bezendu, zgadza się. Rozwiąż (3), Radek zgubił wczoraj rozwiązania, a dzisiaj nie chce się udzielac.

bezendu: 2sin²x−2sin²x*cosx=1−cosx 2sin²x−2sin²xcosx+cosx−1=0 2sin²x(1−cosx)+(cosx−1)=0 2sin²x(1−cosx)−(1−cosx)=0 (1−cosx)(2sin²x−1)=0

	√2		√2
cosx=1 sinx=		lub sinx=−
	2		2

	π		3π		5π		7π
x=0 x=		x=		x=		x=		x=2π
	4		4		4		4

Jeśli nigdzie nie mam błędu. Pierwszego nie wiem jak zrobić (chodzi o zadania dla Piotra)

ZKS: Można było tutaj zauważyć że 2sin²(x) − 1 = −cos(2x). Natomiast zadanie pierwsze dla x ∊ (0 ; π) funkcja jest postaci

	sin2(x) − sin(x)
f(x) =
	sin(x)

f(x) = sin(x) − 1 dla x ∊ (π ; 2π)

	sin2(x) + sin(x)
f(x) =
	sin(x)

f(x) = sin(x) + 1.

Mila: Dobrze. Dlaczego nie ma tam znaków: "∨" Spróbuj z def. wartości bezwzględnej rozpisać wzory w zadaniu (1)

bezendu: Nie chciało mi się klikać ale wiem,że musi być spójnik lub.

sin2x−|sinx|
sinx

sin2x−sinx
sinx

sinx(sinx−1)
sinx

f(x)=sin(x)−1

sin2x+sinx
sinx

sinx(sinx+1)
sinx

f(x)=sinx+1

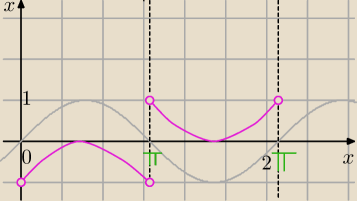
Mila: Brak przedziałów, kiedy tak ma być. (lecą punkty w dół) Zobacz u ZKS, jak ma być.

bezendu: Dziękuję Mila. Dasz mi kilka wskazówek odnośnie zadań z ciągami ?

Mila: Jeśli dzisiaj zdążę, bo jeszcze pół godziny tu jestem. Jutro tez jest dzień. Pisz. Załóż nowy wątek.