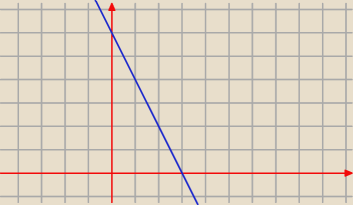
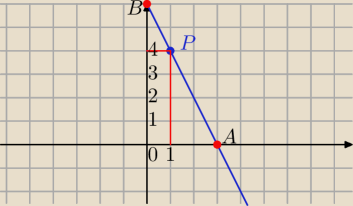
k Radek: Prota o równaniu y=6−2x wraz z osiami współrzędnych wyznacz trójkąt prostokątny ABO. W trójkąt ten wpisano prostokąt w ten sposób, że jeden z wierzchołków prostokąta znajduję się w początku układu wsp. a dwa inne na osiach układu współ. Czwarty wierzchołek lezy na odcinku AB uzasadnij, że pole tego prostokąta nie jest większe od połowy pola trójkąta ABO takich rozwiązań jest kilka ? chodzi o rozmieszczenie punktów ?

Mila: Obierasz punkt P(x,6−2x) na prostej. P_Δ=9 Oblicz pole prostokąta P_▭(x) (w zależności od x) i oblicz największą wartość tej funkcji.

Radek: A=(0,0) B=(x,0) C(x,−2x+6) D=(0,y) tak będę wyglądać punkty ?

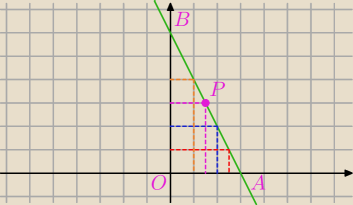
Bizon: punkt P ma współrzędne (x_P, −2x_P+6) Pole powstałego prostokąta S=−2x_P²+6x_P

	−b
Smax... dla xw czyli		xw=−1,5
	2a

S_max=−2*2,25+9=4,5 Zauważ, że pole trójkąta ABO jest równe 9 ... i masz dowód −

Radek: Nie koniecznie chodziło mi o gotowca Pytałem o punkty.

Eta: Nadgorliwość nie popłaca Bizon

Radek: Pani Eto dobre mam współrzędne tych punktów ?

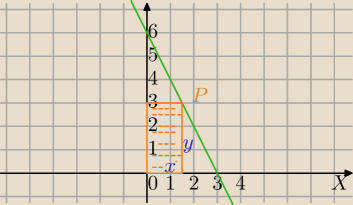
Mila: Jakie są długości boków prostokąta? P(x,y), y=6−2x Punkt P ma wsp. (x,6−2x), 0<x<3⇔6−2x>0 P_▭(x)=?

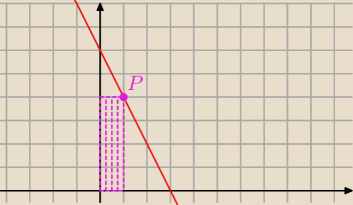
Radek: Ale on może również tak wyglądać ?

Mila: Radek , to co Ci napisałam obejmuje wszystkie przypadki.

Radek: Czyli muszę policzyć długości odcinków aby wyznaczyć to pole ?

Mila: P_▭(x)=x*y⇔ P_▭(x)=x*(6−2x) i masz funkcję kwadratową, wróć do mojego wpisu 21:02

Radek: P=−2x²+6x

	−6
xw=		=1,5
	−4

y_w=4,5

Mila: Teraz komentarz i odpowiedź.

Radek: Ale jeszcze mam pytanie czemu bok ma długość 6−2x ?

Mila: Jeden bok to współrzedna x−owa, a drugi to współrzędna y−owa punktu P ( albo ich wartości bewzgledne.)

Radek: Bo długość jednego boku to np A=(0,0) B=(0,x) AB=√x²=x ?

Radek: ?

Mila: √x²=|x| Radek, nie komplikuj. P(x,y)=(1,4) P=1*4=4 Masz we wzorze (x,6−2x), bo punkt P ślizga się po prostej od punktu A do B.

Mila: Dobranoc.

Radek: Dziękuję i dobranoc, jutro jeszcze wrócę do tego zadania.