stereometria DADA: Przez punkty A i B leżące poza płaszczyzną π poprowadzono proste prostopadle do tej płaszczyzny, przebijające ją odpowiednio w punktach A' i B' . Wiedząc, że | AA'| = 80 cm i |BB'| = 60 oblicz , oblicz odległość środka odcinka AB od płaszczyzny π. Pani mówiła, że trzeba to zadanie zrobić za pomocą podobieństwa trójkątów ale ja nie zauważam tych zależności. Proszę o pomoc.

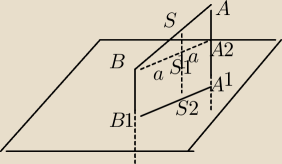
AS: AA2 = AA1 − BB1 = 20 SS1 : a = AA2 : (2*a) => SS1 = AA2/2 = 10 Szukana odległość SS2 = BB1 + SS1 = 60 + 10 = 70

DADA: skąd wiesz że AA2 jest 2 razy większe od SS1?

AS: AA2 jest różnicą odcinków AA1 i BB1

DADA: no to rozumiem ale ty przyjąłeś że SS1 =a natomiast AA2= 2a i tego nie rozumiem

AS: Jeżeli S jest środkiem AB to S1 musi być środkiem BA2 (tw.Talesa)

DADA: ok dzięki tylko taki problem jest że są w odp dwa wyniki jeden ten co obliczyłeś a drugi d = 10

AS: Być może,że 10 odnosi się do odcinka SS1 a dopiero dodanie odcinka BB1 da szukaną odległość.

Mila: II wariant A i B leżą po przeciwnych stronach płaszczyzny π.