równanie trygonometryczne rozwiąż: tg 3x = 1 w zbiorze (0; π) ;
Zosia: równanie trygonometryczne rozwiąż:
tg 3x = 1 w zbiorze (0; π) ;
zał
| | π | |
3x = |
| + kπ /: 3 , k ∊ℂ |
| | 4 | |
| | π | | 1 | |
x = |
| + |
| kπ ∊ (0; π), wtedy i tylko wtedy gdy k ∊ {0,1, 2} − |
| | 12 | | 3 | |
NIE ROZUMIEM SKĄD BIORĄ SIĘ TRZY PUNKTY, MOGĘ PROSIĆ O POMOC. Z CZEGO ONE WYNIKAJĄ
otrzymujemy rozwiązania
16 sty 18:14
Basia: wstawiasz za k odpowiednio 0, 1, 2
x= π/12 + 1/3 * 0 π= π/12
16 sty 18:22
Zosia: tak rozumiem że podstawiam trzy punkty jednak, dlaczego pojawiają się takie liczby w
wyznaczonym przedziale (0, π)
jak odczytać je ewentualnie z wykresu?
16 sty 18:26
16 sty 18:49
Zosia: 

chciałabym zrozumieć skąd biorą się wyniki
16 sty 19:06
kika: gdy masz tgx=1 wtedy w przedziale (0.π) masz tylko kąt 45 stopni następny 45+180
wychodzi poza przedział
W Twoim zadaniu
| | 45 | | k*180 | |
tg3x=1 wtedy 3x=45+k*180⇒x= |
| + |
| i teraz wyliczasz kąty które mieszczą |
| | 3 | | 3 | |
się w podanym przedziale , stąd trzy odp
16 sty 19:12
kika: Posługiwałam sie stopniami dla ułatwienia zapisu
16 sty 19:13
Zosia: Rozumiem, dziękuje.
Jeszcze jedno pytanko wstawiamy kolejne liczby naturalne, tak. Do momentu kiedy odp. nie mieści
się w przedziale.
16 sty 19:23
kika: Tak !
16 sty 19:24
kika: Ponieważ masz przedział (0,π) a w innyk k∊C
16 sty 19:25
Zosia: tak, wynika z założeń (czytanie ze zrozumieniem)

dzięki
16 sty 19:31
kika: 
16 sty 19:35
16 sty 19:40
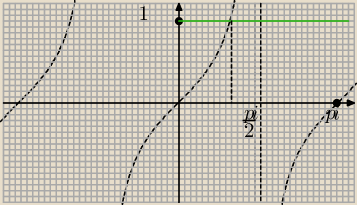

 dlaczego w przedziale (0,π) dla funkcji tg 3x = 1 rozważamy trzy punkty o których wspomniałam
z wykresu nie wynikają trzy punkty tylko 1 w zadanym przedziale
dlaczego w przedziale (0,π) dla funkcji tg 3x = 1 rozważamy trzy punkty o których wspomniałam
z wykresu nie wynikają trzy punkty tylko 1 w zadanym przedziale

 chciałabym zrozumieć skąd biorą się wyniki
chciałabym zrozumieć skąd biorą się wyniki
 dzięki
dzięki



