 stereometria, dero2005, zajrzysz?
1.dany jest prosotkąt o bokach dlugosci 3 i 4. oblicz objetosc bryły powstałej w wyniku tego
prostokąta wokół;
prostej rownoległej do dłuższych boków i odległej od nich odpowiedio o 1cm i 2cm.
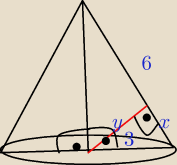
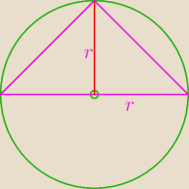
2. w kulę wpisano stozek o promieniu 3cm ktorego przekrojem osiowym jest trojkąt rownoboczny.
oblicz odleglosc srodka podstawy stozka od prostej zawierającej tworzącą stozka
stereometria, dero2005, zajrzysz?
1.dany jest prosotkąt o bokach dlugosci 3 i 4. oblicz objetosc bryły powstałej w wyniku tego
prostokąta wokół;
prostej rownoległej do dłuższych boków i odległej od nich odpowiedio o 1cm i 2cm.
2. w kulę wpisano stozek o promieniu 3cm ktorego przekrojem osiowym jest trojkąt rownoboczny.
oblicz odleglosc srodka podstawy stozka od prostej zawierającej tworzącą stozka
| πr3 | ||
Vstożka= | ||
| 3 |
| 4πr3 | ||
Vkuli= | ||
| 3 |

 ok, dzieki. nie pomyslałem o tym ze moze byc rownoramienny,
kolejne zadanko/
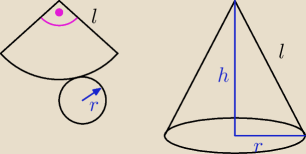
z arkusza blachy w kształcie koła o srednicy 4 cm wycięto wycinek o kącie srodkowym 90 st i
zwinięto go tworząc powierzchnię boczną stożka. Oblicz. promien podstawy stozka, objętosc
stozka, pole przekroju osiowego stozka. robiłem to tak:
ok, dzieki. nie pomyslałem o tym ze moze byc rownoramienny,
kolejne zadanko/
z arkusza blachy w kształcie koła o srednicy 4 cm wycięto wycinek o kącie srodkowym 90 st i
zwinięto go tworząc powierzchnię boczną stożka. Oblicz. promien podstawy stozka, objętosc
stozka, pole przekroju osiowego stozka. robiłem to tak:
| √2 | √2 | |||
ro zwinieciu wycinka mam przekroj stozka gdzie r= | i h= | z tego wynika ze l = | ||
| 2 | 2 |
| √2 | ||
v= | ||
| 12 |
 a = 4
b = 3
I przypadek
r = 1
R = 1+ b = 4
V = πa(R2 − r2) = 60π cm3
II przypadek
r = 2
R = 2+b = 5
V = πa(R2 − r2) = 84π cm3
a = 4
b = 3
I przypadek
r = 1
R = 1+ b = 4
V = πa(R2 − r2) = 60π cm3
II przypadek
r = 2
R = 2+b = 5
V = πa(R2 − r2) = 84π cm3
 l = 2
l = 2
| 90 | |
*2πl = 2πr | |
| 360 |
| 1 | 1 | |||
r = | l = | cm | ||
| 4 | 2 |
| √15 | ||
h = √l2 − r2 = | cm | |
| 2 |
| πr2*h | π√15 | |||
V = | = | cm3 | ||
| 3 | 24 |
| √15 | ||
Po = h*r = | cm2 | |
| 4 |
| α | ||
aaa u mnie w tablicach mam wzor l=2πr* | i to r=l czyli tworzącej stozka, nie zczaiłem | |
| 360 |

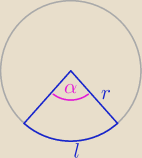 to wszystko zależy od oznaczenia
jeżeli oznaczymy długość łuku przez literę "l" i promień przez literę "r" to wzór na długość
łuku będzie miał postać
to wszystko zależy od oznaczenia
jeżeli oznaczymy długość łuku przez literę "l" i promień przez literę "r" to wzór na długość
łuku będzie miał postać
| α | ||
l = | 2πr | |
| 360 |
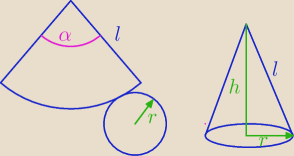 jeśli natomiast rozpatrujemy wycinek koła jako powierzchnię boczną stożka to oznaczamy promień
tego wycinka koła jako "l" gdyż będzie to tworzaca stożka, którą z reguły oznaczamy "l"
natomiast literą r oznaczamy promien podstawy stożka
wtedy długość łuku wycinka kola jest równa długości obwodu podstawy stożka i otrzymujemy wzór
jeśli natomiast rozpatrujemy wycinek koła jako powierzchnię boczną stożka to oznaczamy promień
tego wycinka koła jako "l" gdyż będzie to tworzaca stożka, którą z reguły oznaczamy "l"
natomiast literą r oznaczamy promien podstawy stożka
wtedy długość łuku wycinka kola jest równa długości obwodu podstawy stożka i otrzymujemy wzór
| α | |
2πl = 2πr | |
| 360 |