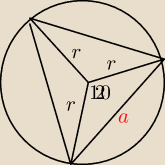
ge Radek: Punkty A = (3,4) , B = (0,3 ) i C = (1,0) należą do okręgu. Oblicz pole trójkąta równobocznego opisanego na tym okręgu. Wyznaczyć równanie okręgu i co dalej ?

kika:

Radek: ?

Radek: Jak wyznaczyć wierzchołki tego trójkata ?

kika: nie musisz

Radek: To nadal nie wiem ?

kika: jeżeli wyznaczysz r−nie okręgu , to masz promień i popatrz na rysunek.

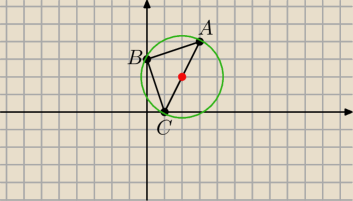
Mila: Wyglada na Δ prostokątny, wtedy środek okręgu opisanego na tym Δ leży w środku AC. BC²=1²+3²=10 AB²=10 AC²=2²+4²=20 Bingo! 20=10+10 Dalej prosto, tylko zrób sobie szkic na brudno.

Eta: 1/ sprawdź najpierw jakim trójkątem jest trójkąt ABC i wszystko się wyjaśni

Eta: Ech Bizon

Radek: Dziękuję. Wgl nie mogę sobie poradzić z tym działem

Mila: Skończyłeś to zadanie?

Radek: Tak. Ale jeszcze potrzebuje pomocy.

Mila: To pisz.

Radek: Pomoże mi dziś Pani ?

Mila: Pomogę, ale nie denerwuj się, jeśli musisz poczekać, bo czasem odchodzę od komputera do innych zajęc.

Radek: Wyznacz wszystkie rozwiązania równania 2sin²x+3cosx=0 w przedziale <0,2π> 2(1−cos²x)+3cosx=0 2−2cos²x+3osx=0 −2cos²x+3cosx+2=0 t=cosx <−1,1> −2t²+3t+2=0 Δ=25 √Δ=5

	−3−5
t1=		=2 nie należy
	−4

	−3+5		1
t2=		=−
	−4		2

	1
cosx=−
	2

	π
x=−
	3

Nie wiem co dalej

Mila:

	1
cosx=		masz serię rozwiązań
	2

	π		−π
x=		lub x=		[cosx jest funkcją parzystą, to znaczy cosα=cos(−α) ]
	3		3

	−1
cosx=		⇔też masz serię rozwiązań,
	2

	1
którą budujesz wykorzystując wiadomości dla cosx=
	2

	π		−π
x=		+π+2kπ lub x =		+π+2kπ⇔
	3		3

	4π		2
x=		+2kπ lub x=		π+2kπ
	3		3

	4π		2π
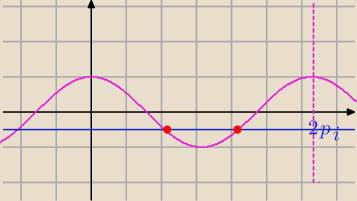
Teraz kolejno : w przedziale (0,2π) mamy:		i
	3		3

dale podstawiasz za k, k=1 i sprawdzasz czy dalsze rozwiązania są w (0,2π). Z wykresu widać, że są dwa rozwiązania w tym przedziale.

Radek: Wiem, że są dwa rozwiązania ale nie rozumiem czemu Pani w rozwiązaniu

	π
x=		dodaje π ?
	3

Mila: Najpierw buduję serię dla cosinusa dodatniego ( to dobrze pamiętam z tabelki, nie chce mi się pamiętać dla ujemnych wartości, to się myli), potem przesuwam o π i jest dobrze. cos 60 =0,5 cos(180+60)=−0,5 cos(−60)=0,5 cos(180−60)=−0,5 wzory redukcyjne.

Radek: Nadal nie rozumiem .

Radek:

	1		π		π
normalnie jak bym rozwiązał cosx=−		to miałbym x=−		+2kπ lub x=		+2kπ
	2		3		3

Mila: Nie miałbys, popatrz na wykres:

	1
cos (−60)=
	2

	1
cos60=
	2

Przeczytaj uważnie co napisałam, zobacz jak nauczyciel rozwiązywał. Przecież cosinus jest ujemny w drugiej i trzeciej ćwiartce.

Radek: Ale ja mam znaleźć rozwiązania w <0,2π>

Mila: (0,2π) to inaczej (0, 360 ^o) i wszystko się zgadza.

Radek: Analizuję ale nie wiem czemu jest dodawane to π ? Dziś na maturze też nie zrobiłem tego zadania a miałem podobne.

Mila: Dała Pani tabelkę dla ujemnych wartości? Uczyła liczyć wartości f. trygonometrycznych dla kątów z II, III IV ćwiartki? Obliczaj: cos 150⁰ sin120^o cos 120^o tg 120⁰

Mila: Gdzie ta matura, co pisałeś, jest w necie?

Radek: Nie miałem tego w szkole.

	√3
cos150=cos(180−30)=−cos30==−
	2

	√3
sin120=sin(180−60)=−sin600=−
	2

	1
cos120=cos(180−60)=−cos60=−
	2

tg120=tg(180−60)=−tg60=−√3

Radek: Nie ma jeszcze arkuszy. Ale poszukam

Mila: sinus źle. wierszyk umiesz?

Mila: A jak Ci dzisiaj poszło?

Radek:

	√3
sin120=sin(180−60)=sin60=
	2

Tak znam.

Radek: Nie zrobiłem jednego zadania z bryłą i tego równania nie dokończyłem. 1. suma sześcianów 3 kolejnych liczb naturalnych i trzeba było pokazać, że jest podzielna przez 9 2. rowiązać równanie z wartośc bez 3, Wielomian z niewiadomymi i wyznaczyć je 4, Ciąg jest arytmetyczny a po dodaniu geometryczny 5, Równanie do stycznych do okręgu przechodzących przez punkt (0,0) 6, Dowód z planimetrii 7. Prawdodpodobienstwo 8. Dowód z planimetrii 9. Funkcja kwadratowa 10. Twierdzenie sinusów i optymalizacja 11, bryła 12 równanie tryg

Radek: Oczywiście równanie stycznej zrobiłem dzięki Pani

Piotr 10: A było jakieś ciekawe zadanie ?

Radek: Same ciekawe, najlepsze z prawdopodobienstwa

Piotr 10: A co z prawdopodobieństwem było ? Z kartami coś czy z czymś innym ?

matuszysta: dowodzenie z planimetrii zawsze bnajgorsze jest ,a tutaj 2 zadania

Radek: Dziennik. Akurat zadania z planimetrii były łatwe

Piotr 10: Ok. Ja to teraz robię arkusze z Pazdro. Dzięki za odpowiedź

Mila: Zobaczymy ,ile dostaniesz punktów, taka maturka jest pożyteczna, będziesz miał wskazówkę, nad czym pracować.

Radek: A wracając do tego zadania co robić dalej ?

Mila: No, już masz rozwiązania tego równania Jeśli nie umiesz ustalić pierwiastków dla ujemnych wartości, to musisz się nauczyć rozszerzonej tabelki dla kątów ∊<0,360) Właśnie dla sinusa i cosinusa szukamy najpierw rozwiązań dla α∊<0,2π> i dodajemy 2kπ. Poszukaj materiałów , w podręczniku też masz wytłumaczone.

Radek: I mam korzystać z tej tabelki jeśli wychodzi rozwiązanie ujemne ? a w dodatnim nie musze pisać +2kπ bo mam przedział <0,2π> ?

Mila: To zależy od równania. np,

	1
sin(4x)=		, piszesz , potem sprawdzasz, które rozwiązania należą do (0,2π )
	2

Radek: Umiem rozwiązywać równania ale jeszcze mam problem z tymi przedziałami. Dziękuję

Mila: Rozwiązuj codziennie po jednym na forum, to może rozwiejesz wątpliwości.

Radek: Dobrze, będę robił tak jak Pani radzi.