Oblicz pochodną, monotoniczność, ekstremum, dziedzinę, asymptoty Pic: Oblicz pochodną, monotoniczność, ekstremum, dziedzinę, asymptoty f(x)=lnx/x

Kejt: w czym problem?

Pic: Nie ogarniem tego a na jutro mi to potrzebne. Dziedzina: x∊(0,+∞) tak ? A dalej

Kejt: tak, a dalej pochodna.. ze wzoru:

	f(x)		f'(x)*g(x)−f(x)*g'(x)
(		)'=
	g(x)		[g(x)]2

napisz ile Ci wyszło

Pic: x=e i co jak to narysowań na osi ?gdzie malejąca a gdzie rosnąca ?

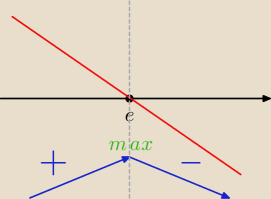
Kejt: więc: dla x∊(−∞;e) f(x)↗ dla x∊(e;+∞) f(x)↘

	1
zmienia znak z + na − a więc mamy maksimum lokalne dla f(e)=
	e

no i zostają asymptoty. czyli musisz policzyć granicę prawostronną dla 0, i sprawdzić, czy są też asymptoty ukośne.. jakieś pytania?

Pic: a ekstrema wyszła: x=e¹/2

Kejt:

	1
mi wyszło.		.. hmm..mogłam się walnąć
	e

fx: "ekstrema wyszła" − co to ma być?