Zbiór A jest zbiorem rozwiązań nierówności x^4 - 2x^3 + 8x - 16 <0. Sprawdź, czy Zosia: Zbiór A jest zbiorem rozwiązań nierówności x⁴ − 2x³ + 8x − 16 <0. Sprawdź, czy liczby a =(log₂ 6)² − log₂ 6 * log₂ 3, b = log 5² − log 5² należą do zbioru A. utknęłam proszę o podpowiedzi. a =(log₂ 6)² − log₂ 6 * log₂ 3 = 2 (log₂ 2+ log₂ 3) − (log₂ 2 + log₂ 3)log₂ 3= (log₂ 2 + log₂ 3)log₂ 3= nie wiem jak dalej b=log 5² − log 5² = (log 5 −log 5)(log 5 + log 5)= proszę o wskazówki, z jakich własności skorzystać

Patronus: log₂6 = log₂2 + log₂3 = 1+log₂3 a = (1+log₂3)² − (1 + log23)log₂3 = 1 + 2log₂3 + log²23 − log₂3 − log²₂3 = 1 + log₂3

Patronus: log5² − log5² = 0

Zosia: a= log₂ 3 + log₂ 3²= log₂ 3³= 3 log₂ 3 − można jeszcze uprościć? b= Dzięki a∉ A b∊ A A∊ (−2,2) − jak wyznaczyć ten przedział skoro mamy do czynienia z wielomianem

Zosia:

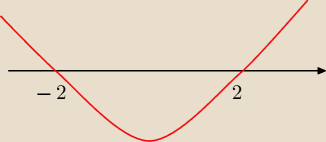
Patronus: x⁴−2x³+8x−16<0 x³(x−2)+8(x−2)<0 (x³+8)(x−2)<0 (x+2)(x²−2x+4)(x−2)<0 x∊(−2;2)

Zosia: więc z rozkładu wielomianu, rozumiem czy można jeszcze uprościć liczbę a?

Patronus: chyba to jest ok, można napisać log₂27 ale to niewiele zmienia

Zosia: ok, dziękuje za pomoc