Pełne badanie funkcji i szkicowanie wykresu.
Pochodne: Mam 2 zadania. Jedno to 'Wyznacz przedziały monotoniczności, ekstrema lokalne, przedziały
wypukłości i wklęsłości oraz punkty przegięcia funkcji' i tam mam 15 podpunktów, a drugie to
'przeprowadź pełne badanie funkcji i naszkicuj wykresy.
I teraz nie jestem pewny, bo jak zrobie zadanie pierwsze to już z samej monotoniczności, PP i
ekstremów mogę naszkicować wykres − to wystarczy? Bo mam wtedy z pierwszej pochodnej ymin i
ymax + wykres z monotoniczności, a później z pochodnej 2 stopnia mam punkt przegięcia i
właściwie już mogę to narysować, więc nie wiem czy jest sens liczenia jeszcze asymptot itd.
15 sty 00:12
Pochodne: Ktoś jest w stanie mi pomóc w tym temacie?
15 sty 01:50
asdf: asymptoty są istotne...
ukośne:
sluza do okreslenia "do jakiej funkcji y = ax+b przybliza sie wykres dla
∞ lub −
∞"
Przypomne, ze czasem trzeba policzyc limes dla −
∞, czasem dla
∞, a czasem jest to ±
∞.
asyptota pionowa wyznaczana jest dla argumentu, ktory nie nalezy do dziedziny. Sprawdzasz wtedy
czy mozna przyblizyc lim
x→x0 f(x) = +/−
∞. tak lopatologicznie to sprawdzasz jaka wartosc
przyjmowala by ta funkcja dla argumentu nie nalezacego do dziedziny funkcji

15 sty 02:15
Pochodne: Czyli oprócz monotoniczności, ektremów lokalnych, punktu przegięcia i przedziałów wypukłości
liczyć jeszcze asymptoty i wtedy dopiero rysować?
15 sty 02:17
asdf: no tak...powinno się zaczyc od liczenia asymptot, może spróbuj:
1
o Policz dziedzine
2
o Policz asymptoty i nanies je na wykres, zaznacz sobie przy okazji jakie wartosci osiaga
funkcja dla +/− inf.
3
o Policz punkty przegięcia, i nanies je na wykres, np. niech f(x) ma punkt przegięcia dla
argumentu x
0 o wartości y
0, to zaznaczasz sobie punkcik (x
0, y
0), np. kolorem zielonym
4
o liczysz wkleslosc / wypuklosc i podobnie jak w pkt 3, tylko teraz kolorem czerwonym.
jak wszystko dobrze policzysz to sie ladnie wszystko zgra

Zaraz Ci podesle rysunek jak to
wygląda
15 sty 02:22
15 sty 02:30
asdf: zaznacz sobie na rgumenta, ze gdzies tam bedzie
zmiana monotonicznosc* powinno być

przegiecie jest dla drugiej pochodnej!
15 sty 02:31
Pochodne: Wielkie dzięki, bardzo mi pomogłeś

15 sty 03:08
daras: a wystarczyło otworzyć podrecznik

np. Macukow, Leksiński − Matematyka w zadaniach
15 sty 08:44

 Zaraz Ci podesle rysunek jak to
wygląda
Zaraz Ci podesle rysunek jak to
wygląda
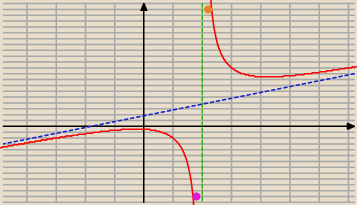 funkcja:
funkcja:
 na koncu ta tabelka, co zaznaczasz jaki ma kształt funkcja.
Warto czasem tez znac punkty przegiecia z osiami
na koncu ta tabelka, co zaznaczasz jaki ma kształt funkcja.
Warto czasem tez znac punkty przegiecia z osiami 
 przegiecie jest dla drugiej pochodnej!
przegiecie jest dla drugiej pochodnej!

 np. Macukow, Leksiński − Matematyka w zadaniach
np. Macukow, Leksiński − Matematyka w zadaniach