Obl najmiejszą wartosć funkcji y=x^2+5x-1 w przedziale JPJP: Obl najmiejszą wartosć funkcji y=x²+5x−1 w przedziale <2;3> a więc p nie należy do przedziału, czyli nei wystarczy policzyć q. Jak zrobić takei zadanie?

asdf: a > 0, czyli ramiona w gore. Musisz wiec policzyc wartosci na krancach, jak sobie rozrysujesz to zrozumiesz o co mi chodzi teraz, taka sytuacja.

Lorak: Jeżeli x_w nie należy do tego przedziału, to sprawdzasz wartości dla iksów z krańców przedziału. Czyli liczysz f(2) i f(3) Mniejsza z nich jest najmniejszą wartością, a większa największą.

JPJP: wychodzi 23

Janek191: a = 1 > 0

	−5
p =		= − 2,5 , więc dla x > − 2,5 funkcja rośnie ( czyli rośnie w całym < 2; 3 > )
	2

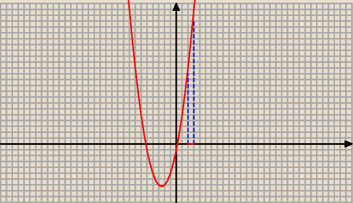
Najmniejsza wartość funkcji, to y_min = f(2) = 2² + 5*2 − 1 = 4 + 10 − 1 = 13 Dodatkowo rysunek