s 1 Zadanie.: Krawędź podstawy ostrosłupa prawidłowego czworokątnego wynosi 8 dm, a wysokość ściany bocznej 5 dm. Oblicz Pc i V

stanisław: Pc = Pp +Pb = a2 + 4*12*a*h = 82 + 2*8*5 = 64 + 80= 144 V = 13*Pp *H = 13*82*3 = 64

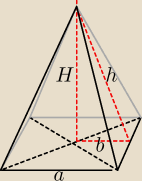
Gembson: Z treści zadania: a = 8dm h = 5dm −−−−−−−−−−−−−−−−−−−−−−−−

	1
W środku ostrosłupa powstaje trójkąt RÓWNOBOCZNY o przyprostokątnych: H i b=		a (a=8 ⇒b=4
	2

) i przeciwprostokątnej h = 5dm 1. POLE POWIERZCHNI POLE POWIERZCHNI OSTROSŁUPA to pole podstawy (kwadrat) i 4 x pole powierzchni bocznej (4xpole trójkąta) Pc = Pp + Pb

	1
Pc = a2 + 4 x (		a x h)
	2

Pc = 64 + 4 x ( 4 x 5 ) Pc = 133 dm² 2. OBJĘTOŚĆ OSTROSŁUPA V = Pp x H z czerwonego trójkąta prostokątnego, na mocy Twierdzenia Pitagorasa obliczam H

	a
H2 = h2 −		2
	2

H² = 25 − 16 H = 9

	a2 x H
V =
	3

	64 x 9
V =
	3

V = 64 x 3 dm³ V = 192 dm³

Gembson: sprawdzę moje obliczenia!

Gembson: UWAGA ODNOŚNIE MOJEGO ROZWIĄZANIA! 1. POLE POWIERZCHNI CAŁKOWITEJ Popełniłem bład przy wpisaniu wyniku ma być 144dm² 2. OBJĘTOŚĆ Podczas obliczania H z Pitagorasa, przez pośpiech zapisałem bez pierwiastka, stąd objętość wyszła 3 razy za duża V = 64 dm³