wykładnicze as8210: Prośba możecie sprawdzić czy to dobrze bo to jest moja praca kontrolna i nie wiem czy dobrze zrobiłam.... Rozwiąż równania wykładnicze: a) (0,5)^3x−4=8^2x+1 (¹₂)^3x−4=((¹₂)⁻³)^2x+1 (¹₂)^3x−4=(¹₂)^−6x−3 3x−4=−6x−3 6x+3x=−3+4 9x=1/:9 x=¹₉ b) (²₃)^x2−3x=(⁹₄)^x−3 (²₃)^x2−3x=((³₂)²)^x−3 (²₃)^x2−3x=(³₂)^2x−6 (²₃)^x2−3x=((²₃)⁻¹)^2x−6 (²₃)^x2−3x=(²₃)^−2x+6 x²−3x=−2x+6 x²−3x+2x−6=0 x²−x−6=0 i teraz delta : D=b²−4ac D=1+24 d=25 czyli pierwiastek z delty to 5 i teraz x1 ,x2 x1 wyszło mi −2 a x2 wyszło mi 3 i mam na końcu napisać że rozwiązaniem jest −2,3 tak ?

as8210: bardzo proszę o sprawdzenie postu z godz 19.54

Jędruś: myślę, że dobrze...

as8210: ale pewności nie masz?

BoosterXS: Wszystko dobrze jest Pozdrówki

PW: b) Sprawdzam dla x=−2:

	2		9
(		)4+6 = (		)−2−3
	3		4

	2		9
(		)10 = (		)−5
	3		4

	2		3
(		)10 = (		)−10
	3		2

− zdanie prawdziwe, −2 jest rozwiązaniem równania. Sprawdzenie dla x=3:

	2		9
(		)9−9 = (		)3−3
	3		4

	2		9
(		)0 = (		)0
	3		4

1=1 − zdanie prawdziwe, 3 jest rozwiązaniem. Odpowiedź: Rozwiązaniami równania są liczby −2 i 3 (inaczej: zbiorem rozwiązań równania jest {−2, 3}). Takie sprawdzenie powinno się robić rutynowo (czy czasem nie otrzymaliśmy głupstwa) − wtedy dopiero sprawdzamy rachunki, czego mi się nie chciało.

as8210: Dzięki bardo ale mam jeszcze inne i nie mogę sobie z nimi poradzić

as8210: nierówność wykładnicza:0,5^2x2−x>1 0,5^2x2−x>0,5⁰ 2x²−x>0 a=2, b=−1, c=0 d=b²−4ac d=1−0 d=1 x1=0 x2=¹₂ dobrze? no i podobno do tago trzeba rysunek a ja nie wiem czy te ramiona to w góre a te kreski gdzie nie wiem...

PW: Zasadniczy błąd: funkcja (0,5)^u jest malejąca, a więc nierówność ... Dlatego zawsze trzeba słowami napisać komentarz o monotoniczności funkcji, a nie "opuszczać podstawy" jak mawia lud.

as8210: nie wiem o co chodzi ...a i jeszcze nie wiem czy to ważne ale tam jest znak >równe ale nie wiedziałam jak to się piszę. Ale to rozwiązane jest dobrze czy źle? o co chodzi ?

PW:

	1
Narysuj wykres funkcji f(u)=(		)u i zobacz, co będzie − czy wiekszym od zera u
	2

odpowiadają większe f(u) niż f(0)=1, czy mniejsze? To jest monotoniczność − im dalej w prawo tym wyżej, albo im dalej w prawo, tym niżej. Jak jest w tym wypadku?

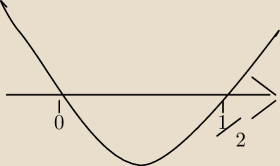
as8210: ale my na zajęciach do tego rysowaliśmy taki wykres czy nie?

PW: Nie mówię o funkcji kwadratowe. Nierówność jest określona jako nierówność dla funkcji wykładniczej. Zajrzyj do podręcznika.

as8210: jak ja nie mam podrecznika

as8210: ale to ....to jest wykładnicz to czemu ma robić kwadratową?

PW: 2^x > 2⁵ Wniosek: x>5, bo funkcja 2^x jest rosnąca. Uczniowie nieraz mówią "opuszczam podstawy", co jest niepoprawne matematycznie i groźne, bo ...

	1		1
(		)x > (		)5,
	2		2

ale wniosek: x <5,

	1
bo funkcja f(x) = (		)x jest malejąca.
	2

Cały czas o tym mówię.

as8210: czy ktoś mi może to jakoś jaśniej wyjaśnić bo nie łapię tego...Jak to ma być?

as8210: bo z ego wszystkiego zrozumiałam tyle że obliczone jest dobrze tylko mam zmienić znak na przeciwny czy nie?

Aga1.: Mówiąc " niepoprawnie matematycznie" Jeśli w podstawie jest ułamek dodatni mniejszy od 1 to opuszczając podstawę należy zmienić kierunek nierówności na przeciwny. U Ciebie (0,5)^2x2−x≥(0,5)⁰ 2x²−x≤0 podstawa należy do przedziału (0,1), 0,5∊(0,1) i dlatego zmieniamy zwrot nierówności na przeciwny. X₁ i x₂ dobrze obliczone. Przy nierówności kwadratowej, (a taką otrzymaliśmy) rysujemy parabolę, która jest poprawnie narysowana. Teraz trzeba podać odp.

	1
Odp. x∊<0,		>.
	2

as8210: czyli dobrze obliczone to fajnie dzięki ale mam jeszcze jeden przykła ale jego to już całkiem nie wiem jak zrobić :8^x(√2)^x−1>(4√2)^2x

Aga1.: doprowadź do podstawy 2. 8=2³ √2=2^1/2 4=2² 8^x(√2)^x−1>(4√2)^2x 2³*2^1/2(x−1)>(2²*2^1/2)^2x Poradzisz sobie dalej?

Aga1.: Powinno być na początku 2^3x

pigor: ..., lub... tak np.: 8^x(√2)^x−1 > (4√2)^2x ⇔ √2 ^6x*√2^x−1 > √2⁴*√2^2x ⇔ ⇔ √2 ^7x−1 >√2 ^4+2x ⇔ 7x−1 >4+2x ⇔ 5x >5 ⇔ x >1 ⇔ x∊(1;+∞) .

as8210: dzięki bardzo sama bym nie dała rady

as8210: przepraszam jeszcze wrócę do godz.9:55 czy ja mam to pisać przy rozwiązaniu "podstawa należy do..........i dla tego zmieniamy zwrot nierównosci na przeciwny . chyba nie co tylko to pod parabolą tak/

J: Nie musisz pisać, jest to tzw. "oczywista oczywistośc"

PW: Musi, musi. Powołanie się na monotoniczność w takich zadaniach (a konkretnie wskazanie że funkcja jest rosnąca albo malejąca) to najważniejszy moment rozwiązania. Jeżeli o tym nie piszemy, to sprawdzający ma dylemat: zrobił dobrze przez przypadek, czy "oczywista oczywistość". Na zasadzie takiej "oczywistości" potem piszą: x⁴ = 2⁴, a więc x = 2, co oczywiście nie jest prawdą (funkcja g(x) = x⁴ nie jest różnowartościowa).

J: Z całym szacunkiem PW.Gdybyśmy w rozwiązaniach zadań, przy kazdym kroku podawali,dlaczego robimy tak, a nie inaczej (cytowali definicje,twierdzenia,własności,itp...),to wkrótce zabrakłoby lasów w Polsce. Jeśli uczeń rozwiązuje nierówność: 2x>4 i pisze 2x>4 ⇔x>2 , to ma skomentowć,że podzielił obustronnie przez 2 ( uzasadniając,że 2 jest rózne od zera ) i nie zmienił znaku nierówności bo 2>0. Nie dajmy się zwariować...Pozdrawiam.

PW: Mylisz się bardzo i podajesz prymitywny przykład, żeby zaciemnić sens. A gdyby podać zbliżony przykład x² < x, to też podzielisz przez x nie komentując, jako "oczywistą oczywistość"?

J: Jeśli podany przez Ciebie przykład, uczeń rozwiązałby dzieląc obustronnie przez x,to oczywiście porazka. Jesli jednak napisze: x²<x ⇔ x²−x<0 ⇔x(x −1)<0 ⇔ ..... to chyba nie Wymagasz od niego, aby uzasadniał kiedy iloczyn dwóch liczb jest ujemny.Przyjmujemy, że on to WIE !, skoro dobrze rozwiązał przykład.

PW: Tak, jeśli rozwiąże dobrze ... czyli napisze x(x−1) < 0 ⇔ (x<0 ∧ (x−1)>0) ∨ (x>0 ∧ (x−1)<0). Wtedy stawiałem piątkę. I niepotrzebne stawało się rysowanie paraboli. Jest to właśnie argumentacja, o którą walczę. Dla mnie najważniejsze w tej sztuce jest uświadomienie sobie "dlaczego tak robimy", a nie przyswojenie nawyków "bo tak się robi". Jasne, że student − rozwiązując ważniejsze problemy − nie musi tłumaczyć poszczególnych kroków. Często piszę się wtedy coś w rodzaju "jak wiadomo rozwiązaniem jest", na zasadzie "Ty wiesz, a ja rozumiem". Jednak na etapie uczenia się o własnościach np. funkcji wykładniczej (na jakim jest pytająca as8210) jest to konieczne. Gdyby poczytać wzorcowe rozwiązania arkuszy maturalnych, to dowiemy się, że ważnym, dającym punkty elementem jest argumentacja − np. przywołanie własności funkcji czy twierdzeń, z których korzystamy.

J: I tu się zgadzamy. Ja też stawiałem piątkę (wtedy maksymalną ocenę).Zgadzam się również z Tobą, że "wypada" podać krótki komentarz przy nietypowym przejściu, np: Jeśli w przykładzie :I I x+4I + 1 I = 5, uczeń napisze ...⇔ Ix+4I + 1 = 5 , to tutaj "prosi" się komentarz: "ponieważ Ix+4I +1 > 0 ", bo nagle pozbywa się zewnetrznej wartości bezwzględnej (nietypowo)

as8210: przepraszam bardzo to pisać czy nie?

as8210: może napiszę