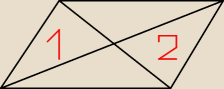
Udowodnij, że Ewa: Dowód geometryczny "Udowodnij, że pola trójkątów są równe." Nie jest nic napisane, że jest to równoległobok, dlatego nie jestem pewna, bo gdyby było z góry powiedziane, że to równoległobok to wiem jak to zrobić Ale tak, to kicha ...

PW: Bez tego ani rusz. Jeżeli jedna z przekątnych została podzielona na odcinki o długościach m₁ i m₂, zas druga na odcinki n₁ i n₂, to pola wskazanych trójkatów są równe

	1		1
		m1n1sinα i		m2n2sinα,
	2		2

jeżeli α jest kątem występującym w obu trójkątach (kąty wierzchołkowe). Musiałoby więc być m₁n₁ = m₂n₂ (przekątne musiałyby dzielić się proporcjonalnie:

	m1		n2
		=		,
	m2		n1

a takiego twierdzenia dla dowolnego czworokąta chyba nie ma. Dla równoległoboku jest to natomiast oczywiste (przekątne dzielą się na połowy).

Ewa: No właśnie! dzięki

PW: A wiesz jakie czworokąty na pewno spełniają warunek zadania? (bo nie tylko równoległoboki).

Ewa: Bodajże trapez równoramienny jeszcze, a jeśli równoległobok to i prostokąt, kwadrat

PW: Tak, dla mnie one wszystkie są trapezami równoramiennymi. Myślę jednak, że tak jest w dowolnym trapezie − "górny" i "dolny" trójkąt są podobne, a więc mają boki odpowiednio proporcjonalne.