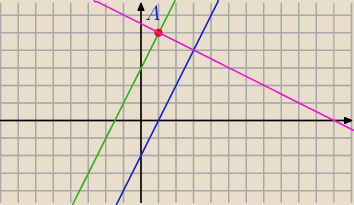
geom analityczna bezendu: Jeden z boków kwadratu ABCD jest zawarty w prostej o równaniu 2x−y−2=0 . Wierzchołek A ma współrzędne (1,5) . Znajdź współrzędne pozostałych wierzchołków wyznaczyłem prostą równoległą do y=2x−2 i przechodzącą przez punkt A⇒y=2x−3 prostą prostopadłą do prostej y=2x−2 i przechodzącą przez punkt A i teraz nie wiem co dalej robić

Bizon: ... "odkładaj" odcinki

bezendu: Będą dwa rozwiązania ?

Bizon: ... oczywiśćie

bezendu: Już inaczej sobie poradziłem z tym zadaniem

5-latek: Podpoweim CI tylko ze przeciez znasz wzor na odledlosc miedzy prostymi rownoleglymi w postaci ogolnej Bedzie to dlugosc boku kwadratu Wydaje tez mi sie ze beda dwa rozwiazania Ale moze jest jeszce inna koncepcja

bezendu: Nie wyszło jednak policzyłem długość odcinka AB=√5 I potem |AD|=√5 √(x−1)²+(2x−3−5)²=√5 ² (x−1)²+(2x−8)²=5 x²−2x+1+4x²−32x+64−5=0 5x²−34x+60=0 ale Δ<0 więc pomysł do bani

bezendu: ?

bezendu: Pomoże ktoś ?

bezendu: up!

bezendu: ?

Bizon: ... i w czym tu masz problem ? Prosta przez A i równoległa do 2x−y−2=0 to y=2x+3 Teraz możesz różnie ... np odległość A od prostej 2x−y−2=0 ... i masz bok Potem na prostej y=2x+3 znajdź punkty odległe od A o długość boku ...,. itd

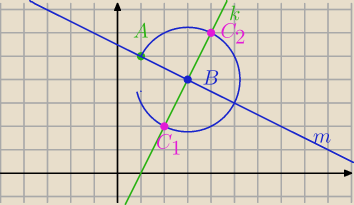
Mila: Jeden z boków kwadratu ABCD jest zawarty w prostej o równaniu 2x−y−2=0 . Wierzchołek A ma współrzędne (1,5) . Znajdź współrzędne pozostałych wierzchołków .

	|2*1−5−2|		5
d=		=		=√5
	√22+1		√5

k: y=2x−2 m⊥k

	−1		−1
y=		x+b, 5=		+b, b=5,5
	2		2

	−1
y=		x+5,5
	2

Punkt przecięcia:

−1
	x+5,5=2x−2
2

x=3, y=4 Kreślisz okrąg o promieniu r=√5 i środku (3,4) (x−3)²+(y−4)²=5 licz dalej

Mila: Dobranoc, jutro sprawdzę.

bezendu: Dziękuję. Dobranoc.

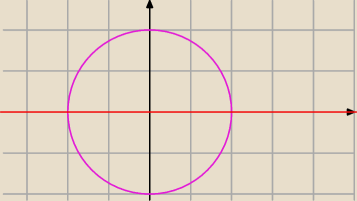
bezendu: To zadnie już wyszło poprawnie.Teraz mam takie: Znajdź zbiór środków wszystkich okręgów stycznych wewnętrznie do okręgu o równaniu x²+y²=4 i stycznych do prostej o równaniu y=0 . S=(0,0) r=2 ?

bezendu: Jakieś pomysły ?

asdf: to co tu narysowałeś to: S(0,0), r = 2?

bezendu: No tak. ?

asdf: dobrze tak chcialem tylko sprawdzic

bezendu:

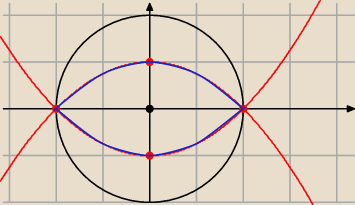
Saizou : "te niebieskie"

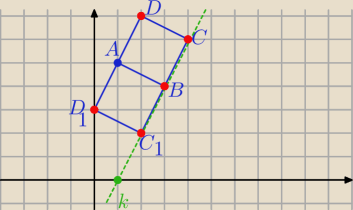
Eta: Można też z wykorzystaniem wektorów: Wektor u ⊥do prostej k : u=[2,−1] i wektor BC⊥u i ponieważ jest to kwadrat to: AB=[ x_B−1, y_B−5]=[2,−1] ⇒ x= 3,y=4 , B(3,4) to z warunku prostopadłości wektorów : BC=[−1, −2] lub [1,2] [x_C−3, y_C−4]= [−1,−2] lub [1,2] ⇒ x_C= 2 i y_C=2 lub x_C= 4 i y_C=6 C₁(2,2) , C₂(4,6) podobnie dla wektora AD =[x_D−1, y_D−5]= [−1,−2] lub [1,2] D₁(2,2) , D₂(2,7)

bezendu: Eta dziękuję za ten sposób a wiesz jak zrobić to 22:15 Możesz wytłumaczyć mi to zadanie ?

bezendu: ?

Saizou: jutro moge to zrobic, bo dzisiaj mi sie juz nie chce

bezendu: Ok. Czyli mam poczekać dokładnie 1 godzinkę ?

Saizou: no dokladnie tylko ze p.m

Godzio: |r₁ − r₂| = |S₁S₂| (warunek styczności wewnętrznej) r₁ = 2, S₁(0,0) (x − x₀)² + (y − y₀)² = r₂² r₂ = |y₀| (to trzeba zauważyć ! ) |2 − |y| | = √x² + y² /² 4 − 2|y| + y² = x² + y² 4 − 2|y| = x²

	1		1
|y| = −		x2 +
	2		2

bezendu: Dzięki Godzio, jutro przeanalizuję

Saizou: za niecala godzine xd a takie ladne zadanko, idealne na mature xd

Eta: Z tym,że: (2−|y|)²= 4−4|y|+y²

Godzio: No właśnie

Eta: No i jeszcze : x∊(−2,2) i y∊(−2,2)

bezendu: Eta wiesz gdzie oprócz matematyka pisz są wytłumaczone wektory ?

Eta: Gustlik podawał ...... poszukaj

bezendu: Będziesz jutro na forum w godz 13−17 ?

Eta: , dopiero po20^oo

bezendu: Kurde

bezendu: Mila czemu robisz za pomocą okręgu to pierwsze zadanie ?

5-latek: Bezendu zdadanie z kwadratem mozesz zrobic tez tak Beda to sposoby dluzsze 1. Masz wyznaczona dlugosc odcinka AB wiec mozesz napisac rownanie prostej rownoleglej do AB w odlegolosci d=√5 Teraz mozesz sobie wyznaczyc punkty przeciecia . Ze wzorow na srodek odcinka wyznaczysz pozostale czyli C₁ i D₁ . 2sposob tez bez wektorow Mozesz wyznaczyc rownanie dwusiecznej miedzy niebieska i rozowa prosta ( w kwadraci jest to przekatna . i masz do wyznaczenia punkty przeciecia

bezendu: ?

bezendu: ?

Mila: Ad1) Można powiedzieć nawyk z konstrukcji. Rozwiązując układ równan: (x−3)²+(y−4)²=5 y=2x−2 Znajdziesz wsp. dwóch punktów: C₁ i C₂. Ja poleciłabym rozwiązanie za pomocą wektorów, ale wiem, że z tym kulejecie, to dałam taki sposób, pięciolatek dodał swoje propozycje.

bezendu: Czasami wychodzą dwa rozwiązania a mi wychodzi jedno i nie wiem gdzie jest błąd.

Mila: W czym tak Ci wychodzi?

bezendu: Zaraz poszukam tego zadania.

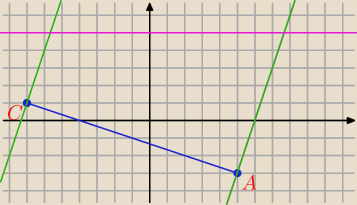
bezendu: Współrzędne przeciwległych wierzchołków prostokąta ABCD są równe A = (5,− 3), C = (− 7,1) . Wyznacz współrzędne pozostałych wierzchołków prostokąta wiedząc, że wierzchołek B leży na prostej y = 5 1⁰ współczynnik AC

	1+3		1
aAC=		=−
	−7−5		3

2⁰ prosta pros, do prostej AC i przez punkt A y=3x−18 3⁰ prosta pros do AC i przez punkt C y=3x+22 4⁰ przecięcie się prostej y=3x−18 i y=5 i potem prosta równoległa do prostej AC i mam wszystkie punkty Ale w rozwiązaniu są dwie wersje

bezendu:

Mila: Napisz ten punkt C, gdybyś znał konstrukcje, to "widziałbyś " więcej. Drugi wariant podpowiem. Jeśli nie zrozumiesz, to napiszę całość.

bezendu: Jaką konstrukcję ? Proszę o całe rozwiązanie

bezendu: ?

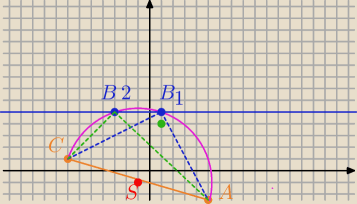
Mila: ΔABC ma być prostokątny, zatem AC jest przeciwprostokątną. S=(−1,−1) środek AC Kreślę okrąg O(S,|SA|), S=(−1,−1), r=√6²+2²=√40 Kąt CB₁A=90^o jako wpisany oparty na średnicy Kąt CB₂A=90^o jako wpisany oparty na średnicy (x+1)²+(y+1)²=40 y=5 x²+2x+1+6²=40 x²+2x−3=0 Δ=16 x₁=−3 lub x₂=1 D₁=(x_d,y_d) S jest środkiem B₁D₁ Dokończysz? II sposób B(x,5) z tw. Pitagorasa CB²+BA²=AC² (x+7)²+(5−1)²+(x−5)²+(5+3)²=(4²+12²) x²+14x+49+16+x²−10x+25+64=16+144 2x²+4x−6=0 x²+2x−3=0 i masz to samo co wyżej.

bezendu: Oczywiście, że dokończę tyko skąd to drugie rozwiązanie mam brać ?

Mila: Przeczytaj uważnie co wcześniej napisałam! B₁=(1,5) i D₁=(xd,yd) S jest środkiem B1D1 B₂=(−3,5) i D₂=(xd,yd) S jest środkiem B2D2 Przekątne dzielą się na połowy.

bezendu: A jeszcze pytanie ? Czy wszystkie takie zadania mam robić, że wpisuję trójkąt w okrąg ?

bezendu: Mila masz jeszcze czas ? Ostatnie zadanie mi zostało ale tym razem do sprawdzenia.

Mila: Nie, przecież podałam Ci II sposób. Musisz wiedzieć, gdzie jest kąt prosty i decydujesz. III sposób − wektory prostopadłe, Etaa, przykładowo rozwiązała.

Mila: Dobranoc. Napisz, jutro dam wskazówki.

bezendu: Mila ja wiem, że podałaś drugi sposób, ale ja pytam ogólnie dla zadań z geometrii analitycznej. A wektorów nie jestem pewny i nie do końca znam więc wolę nie używać.

bezendu: Dziękuję i dobranoc.

bezendu: Nadal jednak nie rozumiem tej konstrukcji.

bezendu: ?

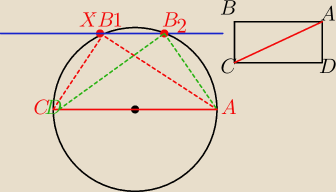
Mila: Masz w zadaniu daną przekątną prostokąta. Ty wystawiłeś w końcach prostopadłe , a przecież boki nie tworzą z przekątną kąta prostego. Zatem nie wiadomo jak te prostopadłe wystawić. AC jest przeciwprostokątną. − patrz prostokąt ABCD Teraz patrz na okrąg. ∡AXC jest kątem wpisanym w okrąg opartym na średnicy, ⇒jest prosty. W zadaniu masz napisane, że B leży na prostej y=5, okrąg przeciął tę prosta w dwóch punktach, to masz dwa rozwiązania, dalej wiadomo jak znaleźć D₁ i D₂.

bezendu: Ale kiedy wiadomo, że będą dwa rozwiązania w zadaniu ? OD czego to zależy ?

Mila: Zależy od zadania, danych. Dobrze jest naszkicować na brudno, wtedy zobaczysz .

bezendu: Dzięki Mila