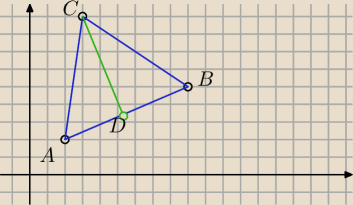
Dane są wierzchołki trójkąta tomek: Dane są wierzchołki trójkąta ABC: A=(2,2), B=(9,5) i C=(3,9). Z wierzchołka C poprowadzono wysokość tego trójkąta, która przecina bok AB w punkcie D. Wyznacz równanie prostej przechodzącej przez punkt D i równoległej do boku BC. Próbowałam zrobić to zadanie chyba z 5 razy i za każdym razem nie mogłem go wyliczyć. Robiłem tak: 1. Znalazłam równanie prostej AB 2. Następnie równanie wysokości opuszczonej na ten bok 3. Z układu równań próbowałem wyliczyć punkt D. 4. Znalazłem równanie prostej CB 5. I na koniec równanie prostej przechodzącej przez punkt D i równoległej do CB I za nic nie może mi to wyjść, bo wychodzą mi jakieś kosmiczne wyniki.

dero2005: 1) wyznaczam współczynnik kierunkowy AB

	yB−yA		3
aAB =		=
	xB−xA		7

2) wyznaczam równanie AB

	3		8
yAB = aAB(x−xA)+yA =		x +
	7		7

3) wyznaczam współczynnik kierunkowy CD

	−1		7
aCD =		= −
	aAB		3

4) wyznaczam równanie CD

	7
yCD = aCD(x−xC)+yC = −		x + 16
	3

5) wyznaczam współrzędne pktu D y_AB = y_CD

3		8		7
	x +		= −		x + 16
7		7		3

tu wychodzi dziwny wynik

tomek: właśnie, punkt D wychodzi dziwny i dalej już nie liczyłem. ale równania wyszły mi tak samo

Eta: Zobacz czy dobrze napisałeś współrzędne punktów ( bo też mam takie wyniki) No cóż licz dalej... liczba , jak to liczba może być i "kosmiczna"

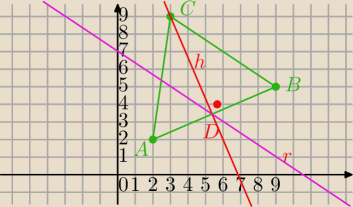
Mila: A=(2,2), B=(9,5) i C=(3,9). Prosta AB: y=ax+b 5=9a+b 2=2a+b odejmuję stronami: 3=7a

	3		3		6		8
a=		, b=2−2*		=2−		=
	7		7		7		7

	3		8
AB: y=		x+
	7		7

Prosta CD:

	7
h: y=−		x+b i C∊prostej h
	3

	−7
9=		*3+b⇔9=−7+b, b=16
	3

	7
h: y=−		x+16
	3

Punkt D:

	7		3		8
−		x+16=		x+
	3		7		7

	156		7		156		16		13		100
x=		, y=−		*		+16=−12−		+16=3		=		,
	29		3		29		29		29		29

Prosta CB :B=(9,5) i C=(3,9). y=ax+b 5=9a+b 9=3a+b −4=6a

	−2
a=		, b=5−9*(−2/3)=5+6=11
	3

	−2
y=		x+11 /*3
	3

3y=−2x+33⇔ 2x+3y−33=0 równanie w postaci ogólnej prosta równoległa: 2x+3y+C=0 Podstawiamy wsp. punktu D

	156		100
2*		+3*		+C=0
	29		29

312		300
	+		=−C
29		29

	612
C=−
	29

	612
r: 2x+3y−		=0 szukane równanie:
	29

Może źle przepisałaś dane i dlatego takie rachunki?

tomek: to jest nowa matura 2015 zadanie 32, http://www.cke.edu.pl/images/files/Matura_2015/Matura2015_Przykladowe_zad/matematyka_PP/matematyka_PP_A1.pdf

Mila: Korzystam z równania ogólnego prostych: II sposób AB^→=[7,3] Prosta h (CD): 7x+3y+C=0 podstawiamy wsp. punktu C=(3,9). 7*3+3*9+C=0 21+27+C=0 C=−48 h: 7x+3y−48=0 Prosta AB⊥h 3x−7y+C=0 podstawiam wsp.A=(2,2) 3*2−7*2+C=0 −8+C=0, C=8 AB: 3x−7y+8=0 Wsp. punktu przecięcia 3x−7y+8=0 7x+3y−48=0

	156
x=
	29

	100
y=
	29

I teraz równanie równoległej do CB jak przedtem