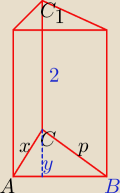
. Piotr 10: Podstawą graniastosłupa prostego jest trójkąt ABC, w którym kąt BAC=30, kąt ACB=105 i długość wysokości CC₁ wynosi 2 cm. Przekątna ściany bocznej o najmniejszym polu tworzy z płaszczyzną podstawy kąt alfa=45. Oblicz objętość tego graniastosłupa.

	2
tg450=
	x

x=2

	y
sin300=
	2

y=1

	1
sin450=
	p

p=√2

	1		√2+√6		1+√3
PΔ=		*2*√2*		=
	2		4		2

V=1+√3 jednak w odpowiedzi jest, że V=2(1+√3) i nie wiem co robię źle

Eta:

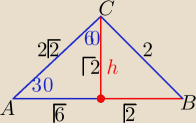
	1		1
Pp=		*(√6+√2)*√2=		*√2(√3+1)*√2 = (√3+1)
	2		2

V=......

Piotr 10: A ok, źle przyjąłem bok Bok naprzeciwko najmniejszego kąta ma najmniejszą wartość U{a}{sinα)=2*R Dziękli