Błagam pomóżcie:((( pilne Kinga: Witajcie, potrzebuję mieć te zadania wyliczone pilnie, bo to na zaliczenie z matmy, a ja kompletnie tego nie kumam, pomóżcie 1. Dany jest sześcian o krawędzi a=4 cm a) narysuj siatkę tej bryły b) oblicz pole powierzchni i objętość tej bryły c) oblicz sumę długości wszystkich przekątnych tej bryły 2. Podstawa prostopadłościanu na wymiary a=3cm, b=4cm, a jego przekątna d=13cm a) narysuj siatkę tego prostopadłościanu b) oblicz pole powierzchni całkowitej i objętość tej bryły 3. Oblicz pole powierzchni całkowitej ostrosłupa prawidłowego trójkątnego, wiedząc że jego krawędź boczna ma długość 18 cm, a promień okręgu opisanego na podstawie wynosi 8cm 4.Oblicz objętość i pole powierzchni całkowitej ostrosłupa prawidłowego trójkątnego, którego krawędź podstawy ma długość 2cm, a ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 60stopni. 5. Wysokość ostrosłupa jest równa 15cm. Obwód jego podstawy wynosi 24cm. Oblicz objętość tego ostrosłupa, jeśli jest to ostrosłup prawidłowy a) czworokątny b) trójkątny c) sześciokątny

5-latek: Tylko nie mow ze na jutro Przeciez to trzeba conajmniej tydzien czasu siedziec przy tym

Kinga: No właśnie na jutro, ale to i tak nie jest wszystko

dero2005: zad5 a)

	24
a =		= 6
	4

P_p = a² = 36

	Pp*H
V =		= 180 cm3
	3

b)

	24
a =		= 8
	3

	a2√3
Pp =		= 16√3
	4

	Pp*H
V =		= 80√3 cm3
	3

c)

	24
a =		= 4
	6

	3a2√3
Pp =		= 12√3
	2

	Pp*H
V =		= 60√3 cm3
	3

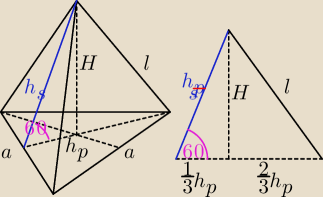dero2005: zad 4 a = 2

	a√3
hp =		= √3
	2

1   hp 3		1
	= cos 60o =
hs		2

	2		2
hs =		hp =		√3
	3		3

H		√3
	= sin 60o =
hs		2

H = 1

	a2√3
Pp =		= √3
	4

	3
Pb =		a*hs = 2√3
	2

P_c = P_p +P_b = 3√3

	Pp*H		√3
V =		=
	3		3

Kinga: dziękuje

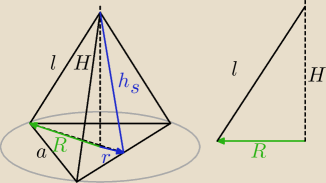dero2005: zad 3 l = 18 cm R = 8 cm

	2		a√3
R =		hp =		= 8 a = 8√3
	3		3

	1		a√3
r =		hp =		= 4
	3		6

H = √l² − R² = √260 = 2√65 h_s = √H² + r² = 2√69

	a2√3
Pp =		= 48√3
	4

	3
Pb =		a*hs = 72√23
	2

P_c = 24(2√3+3√23) sprawdź obliczenia

5-latek: Dero2005 jeszce wkopiesz dziewczyne bo dostanie 6− ke

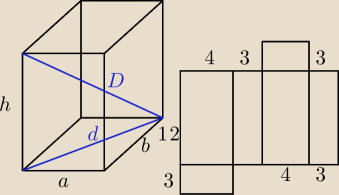dero2005: a = 3 b = 4 D = 13 d = √a² + b² = 5 h = √D² − d² = 12 P_c = 2(a*b+a*h+b*h) = 192 V = a*b*h = 144

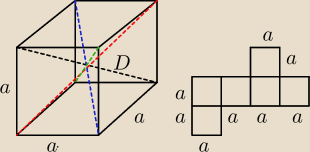dero2005: a = 4 cm D = a√3 = 4√3 cm P_c = 6a² = 96 cm² V = a³ = 64 cm³ ∑D = 4D = 16√3 cm