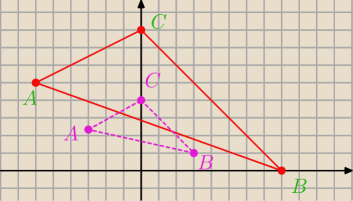
jedomkładnośc bezendu: Wierzchołkami trójkąta ABC są punkty A=(−6,5) B=(6,2) C=(0,8) Trójkąt A'B'C' jest obrazem trójkąta w jednokładności o środku S i skali k>0 jeden z wierzchołków trójkąta A'B'C' jest punkt B'(3,1) wiedząc, że pole A'B'C' jest równe 12 wyznacz skalę k, współrzędne S oraz A' C' A'(−3;2,5) C'=(0,4)

PW: Obliczyłeś pole trójkąta ABC?

bezendu: 27 pole ABC

MQ: 1. Policz pole ΔABC −−> z tego wyznaczysz k. 2. Z B i B', mając k wyznaczysz S, np. SB^→=kSB'^→

bezendu:

	12
k2=
	27

	2
k=
	3

bezendu: ?

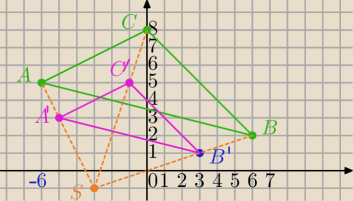
Mila: A=(−6,5) B=(6,2) C=(0,8) S=(a,b), B'(3,1) AC^→=[6,3] AB^→=[12,−3]

	1		1
PΔABC=		|6*(−3)−3*12|=		*|−18−36|=27
	2		2

	2
k=
	3

SB'^→=[3−a,1−b] SB^→=[6−a,2−b]

	2		2
SB'→=		SB→⇔[3−a,1−b]=		*[6−a,2−b]⇔
	3		3

3(3−a)=2*(6−a) i 3(1−b)=2*(2−b)⇔ S(a,b)=(−3,−1) Dalej licz sam . A'=(−5,3) C'=(−1,5) Możesz korzystać z gotowego wzoru na współrzędne po przekształceniu: x'=k(x−a)+a y'=k(y−b)+b

bezendu:

	ΔA'B'C'
Skala jednokładności to k2=		?
	ΔABC

Mila: Tak, dobrze było policzone, to nie powtarzałam.

bezendu: Teraz już sobie poradzę,dziękuję.

Mila: