przebieg zmiennosci funkcji pochodne Alois~: Badanie przebiegu zmienności funkcji trygonometria i się gubię 1. 2tgx tg²x cosx≠0

	2cosx−2sinx
pochodna mi wyszla		pytanie czy dobrze
	cos3x

2(cosx−sinx)=0 cosx=sinx dla π/4 i 5/4π ale co z tym dalej o ile jest dobrze ? (a raczej jest źle) 2. 2sin(x+1/6π)cos(x−1/3π) pochodna jaka mi wyszla = 2cos(x+1/6π)cos(x−1/3π)+2sinx+1/6π))(−sin((x−1/3π)) 3. sin2x + 2 sin(1/4π−x) pochodna jaka mi wyszla cos2x +2cos(1/4π−x) cos2x=0 x=π/4 x=3/4π cos(1/4π−x)=0 x=−1/4π x=−5/4π ... i nie wiem

Alois~: może ktoś zerknąć ?

Alois~: proosze

Alois~: up up

Alois~: zjadło minus 2tgx− tg2x

Alois~: jeszcze podbije

Maslanek:

	2−2tgx
1. Pierwsza pochodna dobra. Łatwiej w zapisie wygląda jako		, ale to jak kto
	cos2x

woli 2. OK 3. źle (sin2x+2sin(...−x))'=2cos2x−2cos(...−x) Jeszcze pochodna funkcji wewnętrznej (−1)

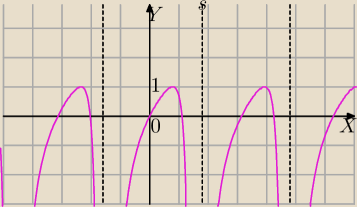Mila: 1) f(x)=2tg(x)−tg²(x)

	π
D: x≠		+kπ, k∊C
	2

2) miejsca zerowe: 2tg(x)−tg²(x)=0⇔ tgx*(2−tgx)=0 tgx=0 lub tgx=2 x=0+kπ lub x=arctg(2)≈63^o 3)Monotoniczność, ekstrema.

	2		2tgx		2−2tg(x)
f'(x)=		−		=
	cos2x		cos2x		cos2x

f'(x)=0⇔2−2tgx=0 tgx=1

	π
x=		+kπ
	4

f'(x)>0⇔2−2tgx>0⇔ tgx<1

	π		π
x∊(−		+kπ,		+kπ) funkcja rosnąca
	2		4

	π
x=		+kπ maksimum,
	4

	π		π
ymax=2tg		−tg2(		)=1
	4		4

	π		π
x∊(		+kπ,		+kπ) funkcja malejąca
	4		2

Mila: Widzę, że nie jest już potrzebne.

Alois~: przybywam baardzo dziękuję Mila

Mila: 2 i 3 MOże udałoby Ci się przedstawić prościej te funkcje.

	A+B		A−B
sinA+sinB=2*sin		*cos
	2		2

A+B		π
	=x+
2		6

A−B		π
	=x−
2		3

Dalej samodzielnie pracuj.