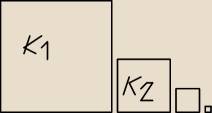
Wyznacz pole kwadratu Pa: Hej Kwadrat K₁ ma bok długości a. Obok niego rysujemy kolejno kwadraty K₂, K₃, K₄, ... takie, że kolejny kwadrat ma bok połowę mniejszy od boku poprzedniego kwadratu. Wyznacz pole kwadratu K₁₂.

Agnieszka : pierwszy kwadrat ma długość boku a, drugi kwadrat ma długość boku a/2, trzeci kwadrat ma długość boku a/4, czwarty kwadrat ma długość boku a/8.... to dwunasty kwadrat będzie miał krawędź o długości a/2048. Pole kwadratu to długość boku² , czyli (a/2048)²

Aga1.: P₁=a²

	1		1
P2=(		a)2=		a2
	2		4

	1		1
P3=(		a)2=		a2
	4		16

	1
Długość boku kolejnych kwadratów tworzą ciąg geometryczny w którym a1=a, q=
	2

	1		1		1
a,		a,		a,		a...
	2		4		8

Oblicz a₁₂ i podnieś do kwadratu.

Pa:

	a
Tak właśnie wyliczyłam, ale zupełnie nie zgadzał mi się wynik		i to jeszcze do
	2048

	a2
kwadratu dało mi		i to dla mnie jakieś nie realne w ogóle.
	4194304

	a2
Czyli mam zostawić w postaci (		) ?
	2048

Aga1.: Ostatnia linijka źle.

	1		a
a12=a*(		)11=
	2		2048

	1
P=a2*(		)2=
	2048

Jeśli dobrze podniosłaś do kwadratu to ok.