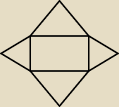
1.Na bokach prostokąta o obwodzie 100cm dorysowano trójkąty równoboczne. Jakie powinny byc
długosci boków prostokąta, aby pole otrzymanej figury było najmniejsze
2.Drut o dł. 100cm podzielono na dwie częsci: z jednej zbudowano kwadratową ramkę, a z drugiej
okrąg. Jaka powinna byc długosc każdej częsci, aby suma pól figur ograniczonych drutem była
najmniejsza
3.Drut o długości 2m podzielono na dwie częsci: z jednej zrobiono kwadratową ramkę, a z drugiej
ramkę prostokątną, w której jeden bok prostokąta ma dlugosc 3 razy wieksza od długosci
drugiego boku. Jak należy podzielic drut, aby suma pól kwadratu i prostokąta była najmniejsza?
4.Drut dł. 8m podzielono na dwie częsci: z jeden zrobiono kwadratową ramkę w kształcie trójkąta
równobocznego. Jak nalezy podzielic drut, aby suma pól kwadratu i trójkąta była najmniejsza
| √3 | √3 | |||
P(b)figury=(50−b)*b+2*b2* | +2*(50−b)2* | |||
| 4 | 4 |
| 100−b | ||
( | )2−−−−−Pkwadr. | |
| 4 |
| b | ||
2TTr=b⇒r= | ||
| 2TT |
| b | ||
Pkoła=TT( | )2 | |
| 2TT |
| 100−b | b | |||
P(b)suma=( | )2+TT( | )2 | ||
| 4 | 2TT |
!
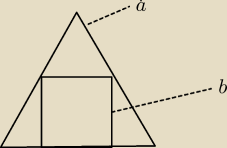4)
a może to nie jest śmieszne,tylko autor miał na myśli sytuację z rys.:
a−−−−−−kształt trójkąta równobocznego
b−−−−−−kwadrat w kształcie trójkąta równobocznego 
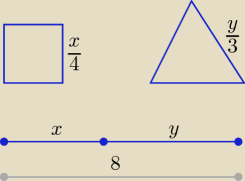Zad. 4. x + y = 8 ⇒ x = 8 − y
| x | 1 | 1 | 1 | |||||
Pole kwadratu PK = ( | )2 = | x2 = | (8 − y)2 = | (64 − 16y + y2) | ||||
| 4 | 16 | 16 | 16 |
| 1 | ||
PK = 4 − y + | y2 | |
| 16 |
| 1 | y | √3 | ||||
Pole trójkąta równobocznego PT = | *( | )2√3 = | y2 | |||
| 4 | 3 | 36 |
| 1 | √3 | |||
Suma pól kwadratu i trójkąta P = PK + PT = 4 − y + | y2 + | y2 → min | ||
| 16 | 36 |
| 1 | √3 | |||
Otrzymaliśmy funkcję kwadratową P(y) = ( | + | )y2 − y + 4 | ||
| 16 | 36 |
| 1 | |||||||||||||||||
minimum w wierzchołku dla odciętej y = | |||||||||||||||||
|
| 1 | 1 | 72 | |||||||||||||||||||||||||||||||
y = | = | * | = | ||||||||||||||||||||||||||||||
|
| 72 |
| 72 | ||
= | ||
| 9 + 4√3 |
| 72 | ||
x = 8 − y = 8 − | = ... | |
| 9 + 4√3 |
