Prawdop Radek: Rzucamy 3 razy kostką do gry. Oblicz prawdopodobieństwo, że kolejno otrzymane liczby utworzą ciąg arytmetyczny.

	18		1
P(A)=		=
	216		12

A=(1,1,1) (1,3,5) (1,2,3) (2,2,2) (2,3,4) (2,4,6) (3,3,3) (3,4,5) (3,2,1) (4,4,4) (4,5,6) (4,3,2) (5,5,5) (5,4,3) (5,3,1) (6,6,6) (6,4,2) (6,5,4)

Mila: Tak.

Saizou : jak dla mnie

saper myli się tylko 1: Jeżeli za zdarzenia elementarne przyjmiemy trójki wyrzuconych oczek (uwzględniamy kolejność), to |Ω | = 63. Wypiszmy zdarzenia sprzyjające. (1,1,1),(2,2,2),(3,3,3 ),(4 ,4,4),(5,5,5),(6,6,6) (1,2,3),(2,3,4),(3,4,5 ),(4 ,5,6) (3,2,1),(4,3,2),(5,4,3 ),(6 ,5,4) (1,3,5),(2,4,6) (5,3,1),(6,4,2). Mamy zatem p =¹₁₂

saper myli się tylko 1: wiesz moze jak to zrobic Wykaż ,że liczba 3√9+4√5+ 3√9−4√5 jest liczbą naturalną

Radek: W urnie jest pewna liczba kul białych i jedna kula czarna. Losujemy jedną kulę z tej urny, zatrzymujemy ją, a następnie z pozostałych kul losujemy jedną kulę. Ile powinno być kul

	2
białych w urnie, aby prawdopodobieństwo wylosowania dwóch kul białych było równe
	3

n−1		n−2		2
	*		=		?
n		n−1		3

Radek: Saper spisać z internetu też potrafię spisałeś dokładnie słowo w słowo.

saper myli się tylko 1: no tak myślałem ,ze pomogę

Radek: ?

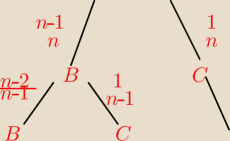
Eta: Hej Radek dobrze A bez tego "krzaka" n −−− ilość wszystkich kul n−1 −−− ilość kul białych 1 −−− kula czarna |Ω|=n*(n−1) A= {(b,b)} to |A|= (n−1)*(n−2)

	(n−1)(n−2)		n−2
P(A) =		=
	n(n−1)		n

	n−2		2
		>		n >2 i n€N
	n		3

teraz dokończ...

Radek: Witam Panią. Mam jeszcze kilka zadań.

Radek: Grupa 2N chłopców i 2N dziewcząt podzieliła się losowo na 2 równoliczne grupy. Jakie jest prawdopodobieństwo, że w każdej z tych grup jest tyle samo chłopców co dziewcząt? Od czego to zacząć ?

Mila: Wskazówka. 2N+2N=4N liczba wszystkich osób Musisz wybrać N chłopców ze zbioru 2N Musisz wybrać N dziewcząt ze zbioru 2N Nie jest ważna kolejność.

Radek:

2N 2		2N 2		(2n−2)!(2n−1)2n		(2n−2)!*(2n−1)2n
	*		=		*		?
				(2n−2)!*2!		(2n−1)!*2!

(2n²−n)*(2n²−n) ?

Eta: Nie .... zobacz co napisała Mila

Radek:

2N N		2N N
	*		?

Eta: ok teraz jeszcze |Ω|=.......

Radek: |Ω|=4N ?

Eta: Nie.... wybierasz grupę 2N z 4N |Ω|=.....

Radek:

4N 2N
	?

Eta: Tak ( bo grupy miały być równoliczne) teraz dokończ P(A)=.... (wynik na literkach)

Radek:

(2N!)4
(N!)4*4N!

dziwnie ?

Radek: Jeszcze mam takie zadanie ale nie wiem czy to jest poprawnie:

	x4−4x2+x+6
Wyznacz wszystkie liczby całkowite x dla których wartość wyrażenia		jest
	x+2

liczbą całkowitą D=R\{−2}

x4−4x2		x+2+4
	+
x+2		x+2

x2(x−2)(x+2)		4
	+1
x+2		x+2

	4
x2(x−2)+1
	x+2

x+2=1 lub x+2=−1 lub x+2=−2 lub x+2=2 lub x+2=−4 lub x+2=−4 o to chodzi ?

Radek: ?

Eta: ok

Godzio: O to

Radek: Dzięki a to zadanie wyżej ok ?

Aga1.:

	4
Wyrażenie można zapisać tak x3−2x2+1+
	x+2

I brakuje x+2=4

Radek: Dzięki Aga1 czyli mogę sobie tak przekształcać a co jeśli wielomian w liczniku miałby pierwiastek ? i dało by się go rozłożyć na czynniki

Mila:

	(2N!)4
1)
	(N!)4*(4N)!

2) O to chodzi, tylko ma być

	4
x2(x−2)+1+
	x+2

I dwa razy masz x+2=−4 i pamiętaj, że x≠−2

Eta: Najprościej to wykonać dzielenie : Licznik : mianownik

	Reszta
i otrzymasz P(x)+
	mianownik

Radek: Dziękuję.

Aga1.: Wydaje mi się ,ze wielomiany są tak dobierane, by było dzielenie z resztą.