szereg koszi: Witam , próbowałem rozwiązać taki szereg wieloma sposobami przeważnie porównują coś do czegoś , ale nie może mi nic wyjść z porównawczego ilorazowego też próbowałem i nie wychodzi bo mi tam granica zero wychodzi a porównywałem go to rozbieżnego, bardzo proszę o pomoc zbadać szereg:

	1		π
∑ sin		* tg
	3√n		√n

n dązy do nieskończoności od jedynki , proszę o pomoc

MQ: Dla dostatecznie dużych n zachodzi:

1		π		1		π
	*		≤sin		*tg
23√n		√n		3√n		√n

koszi: a znak równości nie powinien być na odwrót ? bo nie wydaje mi sie że jest taka zależność : sinx ≤ x , ?

koszi: a w skąd sie wzięła ta dwójka w mianowniku ?

MQ: Ta dwójka w mianowniku, jest właśnie po to, żeby było ≤sinx

	1
dla x−−>0		x≤sinx≤x
	2

koszi: ale napewno jest taka zależność ? bo jeśli tak to jak dobrze rozumiem bo nie wiem czy można tak robić że jeśli jeden szereg jest rozbieżny i ten drugi który też wziąłes z tej zależności jest rozbieżny to ich iloczyn jest również rozbieżny ? no bo jeśli tak to wtedy na mocy kryterium porównawczego wychodzi że ten dany mój szereg jest rozbieżny , dobrze to rozumuje ?

koszi: ale napewno jest taka zależność ? bo jeśli tak to jak dobrze rozumiem bo nie wiem czy można tak robić że jeśli jeden szereg jest rozbieżny i ten drugi który też wziąłes z tej zależności jest rozbieżny to ich iloczyn jest również rozbieżny ? no bo jeśli tak to wtedy na mocy kryterium porównawczego wychodzi że ten dany mój szereg jest rozbieżny , dobrze to rozumuje ?

koszi: ale napewno jest taka zależność ? bo jeśli tak to jak dobrze rozumiem bo nie wiem czy można tak robić że jeśli jeden szereg jest rozbieżny i ten drugi który też wziąłes z tej zależności jest rozbieżny to ich iloczyn jest również rozbieżny ? no bo jeśli tak to wtedy na mocy kryterium porównawczego wychodzi że ten dany mój szereg jest rozbieżny , dobrze to rozumuje ?

koszi: ale napewno jest taka zależność ? bo jeśli tak to jak dobrze rozumiem bo nie wiem czy można tak robić że jeśli jeden szereg jest rozbieżny i ten drugi który też wziąłes z tej zależności jest rozbieżny to ich iloczyn jest również rozbieżny ? no bo jeśli tak to wtedy na mocy kryterium porównawczego wychodzi że ten dany mój szereg jest rozbieżny , dobrze to rozumuje ?

koszi: kurde sory że tyle razy wysłało ale kompa mi zacieło

MQ: Źle rozumijesz, bo z iloczynu dwu wyrazów szeregów rozbieżnych możesz mieć zbieżny, np.:

1		1
	*
n		n

Nie chodzi o to, że są rozbieżne, ale, że ich iloczyn jest rozbieżny:

1		π		π		1
	*		=		*
23√n		√n		2		n(5/6)

5		1
	<1, więc ∑		jest rozbieżny
6		n(5/6)

koszi: no ok ale czy jest taka zależność z tangensem jak z sinusem , mam na myśli , tgx≤x ?

MQ: x≤tgx dla x−−>

MQ: x−−>0 miało być

koszi: a i jeszcze znalazłem taki wzór, że : sinx < x , dla x>0

	2		π
sinx >		x , x ∊(o;		)
	π		2

	1
czy jak to jest z tym sinusem tam ma być		czy to co jest powyżej bo już nie wiem?
	2

a po za tym to czemu jest ten drugi wzór skoro pierwszy z nich zawiera ten drugi a jednak jest

	π
inny bo przecież x>0 zawiera to że x∊(o;		)
	2

MQ: Możesz użyć i tego i tego −− ja po prostu inaczej to oszacowałem.

	π
Ten, co podałeś, to prosta przechodząca przez wartości sinusa w 0 i		. Wykres sinusa leży
	2

ponad nią w tym zakresie.

MQ: Ja dałem ostrzejsze oszacowanie, więc moja zależność jest słuszna w mniejszym otoczeniu 0.

koszi: no ale skąd wiesz że akurat połowa argumentu jest większa od wartości sinusa od tego argumentu , sprawdziłeś jakoś to czy jak to sie dzieje ?

MQ: połowa argumentu jest MNIEJSZA od sinusa w pobliżu zera.

koszi: no tak tam sie pomyliłem miałem na myśli mniejsza, no ale skąd to wiesz ?

MQ: Chociażby stąd:

1		2
	x<		x<sin x
2		π

koszi: no tak ale nie znając tej zależności co ją wcześniej napisałem ?

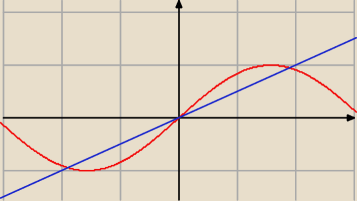
MQ: Wystarczy? A jeśli nie, to:

	sin x
z faktu, że lim(x−−>0)		= 1 i definicji granicy można udowodnić, że dla x
	x

dostatecznie bliskiego 0 |x| < |sin x| lub x < sin x dla x>0

koszi: ok no teraz to wszystko z wykresu , dzięki za odpowiedzi